Klassifikationsbäume

 

Klassifikationsbäume sind ein intuitiver und dennoch leistungsfähiger Algorithmus, um Datensätze auf Basis der Werte kontinuierlicher oder diskreter (kathegorischer) Werte in Klassen zu sortieren. Zusammen mit Diskriminanzanalyse und Logistischer Regression gehören Klassifikationsbäume zu den klassischen Werkzeugen des Kreditscorings. Weiterhin sind sie eine verbreitete Technik des Dataminings, insbesondere in Form von Random Forests, die den Technologien des Machine Learnings zugerechnet werden.

Viele (energie-)wirtschaftlich relevante Fragestellungen laufen auf Klassifikation von Daten hinaus. Beispiele sind:

• Einordnung von Kunden in Bonitätsklassen
• Klassifizierung von Emails: Spam / kein Spam
• Auswahl geeigneter Kunden für eine Direktmailing-Aktion

Für eine solche Klassifikation stehen typischerweise sowohl kontinuierliche Daten wie Umsatz und Ergebniszahlen wie auch kategorische (diskrete) Daten wie Branchenkennzahlen, Postleitzahlen usw. zur Verfügung.

 

Eine klassische Methode Klassifizierungen auf Basis der Werte von kontinuierlichen und diskreten Variablen vorherzusagen, ist der Klassifikationsbaum. Eine klassische Anwendung ist die Erstanalyse von Daten im Rahmen des Dataminings sowie das Kreditscoring von Kunden und Kontrahenten.

Einfaches Beispiel

Für den Einstieg verwenden wir die für solche Demonstrationszwecke allseits beliebten Daten des Titanic-Untergangs (z.B. verfügbar in den Beispieldatensätzen von R). Vorhergesagt werden soll in diesem Fall das Überleben des Passagiers. Die Überlebenswahrscheinlichkeit wird auf Basis von vorliegenden Daten geschätzt. Diese sind:

• Passagierklasse / Crew-Mitglied (Klasse 1-3, 4 = Crew)
• Geschlecht (weibl ja/nein)
• Alter (Kind ja/nein)
• überlebt (ja / nein)

1. Erste Datensichtung

Eine erste Analyse liefert bereits eine Pivot-Tabelle. Schon eine oberflächliche Analyse zeigt, dass alle Daten Einfluss auf die Überlebenswahrscheinlichkeit haben. Hier die (höhere) Überlebenswahrscheinlichkeit von Kindern:

 

	tot	überlebt	Überlebenswahrscheinlichkeit
Kind	52	57	0,52
Erwachsen	1.438	654	0,31

Noch frappierender ist der Unterschied der Überlebenswahrscheinlichkeit von Männern und Frauen an Bord:

 

	tot	überlebt	Überlebenswahrscheinlichkeit
männlich	1.364	367	0,21
weiblich	126	344	0,73

Auch die Passagierklasse hat einen Einfluss:

 

	tot	überlebt	Überlebenswahrscheinlichkeit
1. Klasse	122	203	0,62
2. Klasse	167	118	0,41
3. Klasse	528	178	0,25
Crew	673	212	0,24

 

In diesem Fall sind sowohl die unabhängigen Variablen Passagierklasse, Geschlecht und Alter als auch die zu prognostizierende abhängige Variable, die Überlebenswahrscheinlichkeit, diskrete Variablen. Sie nehmen nur Werte aus einer endlichen Liste an.

2. Klassifikationsbaum des Titanic-Untergangs

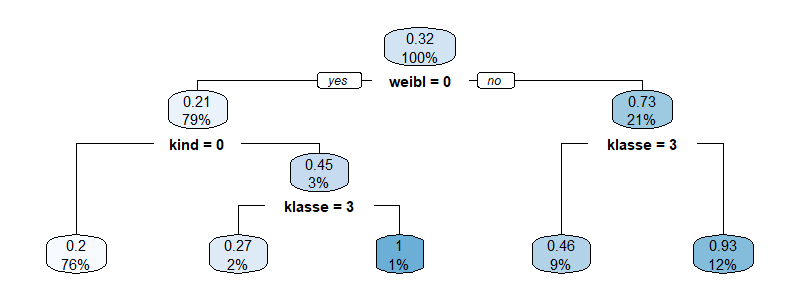
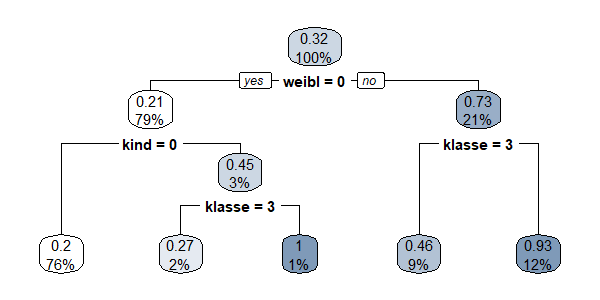
Sind ausreichend Daten vorhanden, so können Wahrscheinlichkeiten für alle Kombinationen der abhängigen Variablen ermittelt werden. Typischerweise nimmt jedoch die Anzahl verfügbarer Daten ab, je mehr unabhängige Variablen bestimmt werden, so dass irgendwann eine weitere Untergliederung nicht mehr sinnvoll ist. Für das betrachtete Beispiel sieht ein Klassifikationsbaum wie folgt aus:

Da nur für einen Bruchteil der Passagiere Rettungsbote vorhanden waren, überlebten im Ergebnis nur ca. 1/3 der Passagiere. Die höchste Überlebenswahrscheinlichkeit hatten männliche Kinder der 1ten und 2ten Passagierklasse (100%), danach kommen Frauen der 1ten und 2ten Passagierklasse und der Crew! (93%), dann Frauen der 3ten Passagierklasse (46%). Männliche Kinder der 3ten Passagierklasse haben immerhin noch eine Überlebenswahrscheinlichkeit von 27%. Erwachsene Männer überlebten nur mit 20% Wahrscheinlichkeit. Der größte Teil der Passagiere (76%) gehört dieser letzten Gruppe an.

Algorithmus

Der Algorithmus (z.B. CART) ist einfach und schnell.

• Der Baum teilt immer in 2 Äste
• an jedem Knoten wird eine Eingangsvariable in zwei Gruppen geteilt, für kontinuierliche Variablen erfolgt dies entlang eines Schwellwerts
• die Trennung erfolgt so, dass die Homogenität der Zielkategorien in den nachfolgenden 2 Knoten maximiert wird
• es wird immer die Variable für den nächsten Split ausgewählt, die zu der größten Zunahme der Homogenität in den nachfolgenden Knoten führt.

Zur Messung der Inhomogenität der Knoten kommen je nach dem konkreten Verfahren verschiedene, nachfolgend beschriebene, sogenannte Metriken in Frage. Um die Abnahme der Inhomogenität zu messen, vergleicht man die Inhomogenität des Mutterknotens mit dem gewichteten Mittelwert der Inhomogenität der Töchterknoten.

1. Varianz

Ein naheliegendes Homogenitätsmaß ist die Varianz. Allerdings kann sie nur bei kontinuierlichen, numerischen Zielgrößen sinnvoll bestimmt werden. Da wir hier vorrangig die Aufteilung eines Datensatzes in Kategorien betrachten, ist die Varianz nicht geeignet.

2. Gini-Index

Der Gini-Index  geht auf den italienischen Statistiker Corrado Gini zurück, der sich insbesondere mit Ungleichheit der Einkommensverteilung beschäftigt hat. Diesen Index verwendet der CART (classification and regression tree) Algorithmus.

 

Der Index misst, wie groß die Wahrscheinlichkeit ist, ein zufällig gewähltes Element eines Knotens fehlerhaft zuzuordnen, wenn man es zufällig entsprechend der Verteilung der Kategorien im Knoten einer Kategorie zuordnet. Der Gini-Index ist Null, wenn alle Datensätze des Knotens in dieselbe Kategorie fallen. Er ist maximal, wenn alle Kategorien innerhalb des Knotens gleichverteilt sind.

 

Für jedes Element eines Knotens sei die Wahrscheinlichkeit, dass es der Kategorie i angehört p_i. Dann ist die Wahrscheinlichkeit, es einer anderen, falschen Kategorie zuzuorden somit 1 – p_i. Somit ergibt sich der Gini-Index für einen Knoten mit J Kategorien als:

Die aggregierte Wahrscheinlichkeit über alle Möglichkeiten zwei Kategorien auszuwählen ist 1, ebenso wie die aggregierte Wahrscheinlichkeit eine beliebige Kategorie auszuwählen:

Hiermit ergibt sich

und somit für den Gini-Index

Der Gini-Index kann auch generell als Güte-Maß verwendet werden, wie gut ein Klassifizierungsalgorithmus Klassen trennen kann.

2. Entropie

Ein weiteres verbreitetes Maß für Inhomogenität ist die Entropie. Für eine Zufallsvariable X mit J möglichen Werten, die jeweils mit einer Wahrscheinlichkeit p_i auftreten, wird sie wie folgt definiert:

Diese Messgröße kann man so motivieren: Hat die Zufallsvariable 2ⁿ gleichverteilte Werte, so benötigt man im Mittel

Ja-Nein-Fragen, um den Wert zu bestimmen. Mit jeder Frage kann man die Menge der Werte halbieren. Somit definiert man den Informationsgehalt der Wahrscheinlichkeit p mit

Die Entropie ist dann der Erwartungswert des Informationsgehalts für eine Zufallsvariable X.

Anwendung im Kreditscoring

Für ein Anwendungsbeispiel im Bereich Kreditscoring verwenden wir einen Datensatz von 1000 deutschen Konsumentenkrediten, der von Professor Dr. Hans Hofmann, Institut für Statistik und Ökonometrie in Hamburg, einstmals zur Verfügung gestellt wurde, und seither vielfach für den Test von Scoringmodellen verwendet wurde. Er ist hier verfügbar.

1. Datensichtung

Die durchschnittliche Ausfallrate ist in dem Datensatz mit 30% extrem hoch. Dies erleichtert die Anwendung statistischer Verfahren aller Art. Vielfach ist die Quantifizierung von Kreditrisiken schon deshalb problematisch, weil für kleinere Kundenklassen keine Ausfälle vorliegen.

 

Die Datei enthält 1000 Datensätze mit vielen Attributen, von denen wir nur die folgenden berücksichtigen möchten:

• Ausfall (0/1)
• Duration (Laufzeit in Monaten)
• Kreditsumme (in DM)
• Girokontostand
  • A11: 0 DM
  • A12 < 200 DM
  • A13 > 200 DM
  • A14 kein Girokonto)
• Kredithistorie
  • A30 bisher keine Kredite
  • A31 alle Kredite pünktlich zurückgezahlt
  • A32 bestehende Kredite bisher pünktlich zurückgezahlt
  • A33 Verzug in der Vergangenheit
  • A34 kritisches Konto / Kredite bei anderen Banken
• in derzeitiger Position angestellt seit
  • A71 arbeitslos
  • A72 < 1 Jahr
  • A73 1-4 Jahre
  • A74 4-7 Jahre
  • A75 >= 7 Jahre
• Position
  • A 171 arbeitslos / unqualifizierte Ausländer
  • A 172 unqualifizierte Inländer
  • A 173 qualifiziert
  • A174 Management / selbstständig / hochqualifiziert
• Ersparnisse
  • A 61 < 100 DM
  • A 62 <= ..< 500 DM
  • A63 500<= < 1000 DM
  • A64 ..>= 1000 DM
  • A65 unbekannt / keine Ersparnisse

2. Modellanwendung

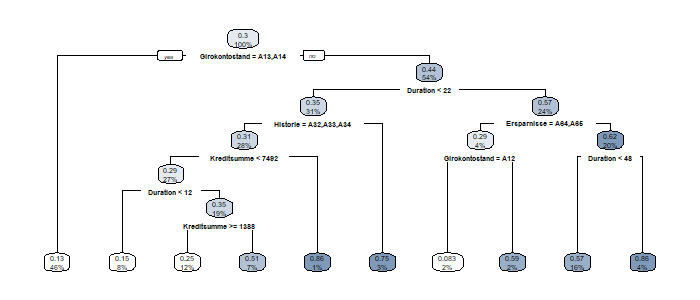
Klassifikationsbäume sind im Paket rpart (bzw. rpart.plot) implementiert. Mit dem folgenden Code erhält man den unten angezeigten Plot:

credit <- read.csv(„http://www.biz.uiowa.edu/faculty/jledolter/DataMining/germancredit.csv“)
cred2 <- credit[, c(„Default“,“duration“,“amount“,“checkingstatus1″, „history“, „employ“, „job“, „savings“)]

require(rpart)
require(rpart.plot)

mdl <- rpart(Default~.,data=cred2)
rpart.plot(mdl)

Erstaunlicherweise gehen die Informationen zum Job überhaupt nicht ein.

3. Gütetest

Eine entscheidende Frage ist natürlich, wie die Güte eines solchen Modells beurteilt werden kann.

 

Um Modellqualität zu testen, benötigt man von den Kalibrierungsdaten unabhängige Testdaten. Da die Richtigkeit von Wahrscheinlichkeiten unterteilt nach Kategorien beurteilt werden soll, darf das Testdatenset nicht zu klein sein. Weiterhin wollen wir die vorhandenen 1000 Datensätze optimal nutzen.

 

Wir gehen somit wie folgt vor:

• der vorhandene Datensatz wird zufällig in drei Teil-Datensätze geteilt.
• einer der Teil-Datensätze wird jeweils als Testdatensatz ausgewählt
• mit den beiden anderen Datensätzen wird das Modell kalibriert
• für jedes Element des Testdatensatzes wird nun mit dem vorher kalibrierten Modell eine Ausfallwahrscheinlichkeit ermittelt
• Diese wird dem tatsächlichen Ergebnis 0 oder 1 gegenübergestellt

Jeder der drei Datensätze wird dabei einmal als Testdatensatz ausgewählt, so dass im Ergebnis für alle 1000 Zeilen der ursprünglichen Datei Istwerte und Prognosewerte auf Basis der drei aus den Trainingsdatensätzen kalibrierten Modellen vorliegen.

 

Da der Klassifikationsbaum als Ergebnis eine überschaubare Anzahl diskreter Wahrscheinlichkeitswerte liefert, kann das Ergebnis in einer Pivottabelle zusammengefasst werden, in der prognostizierten Wahrscheinlichkeiten Ist-Ausfälle und Ist-Rückzahlungen und somit auch eine Istwahrscheinlichkeit gegenübergestellt werden. Mit jedem Testdatensatz wird dabei die Güte des Modells getestet, dass aus dem zugehörigen Trainingsdatensatz erstellt wurde. Der gesamte Datensatz von Prognose- und Istdaten gibt einen Eindruck von der Brauchbarkeit des Verfahrens im Allgemeinen.

 

Die Kalibrierung erzeugt bei unterschiedlichen Trainingsdatensätzen unterschiedliche Bäume und Wahrscheinlichkeitsklassen. Die Gesamttabelle wird somit mit knapp 40 Zeilen schon relativ groß. Eine erste Einschätzung liefert die Korrelation zwischen Forecast-Wahrscheinlichkeit und Ist-Wahrscheinlichkeit. Sie beträgt hier 85 %. Dies zeigt, dass das Verfahren grundsätzlich anwendbar ist.

 

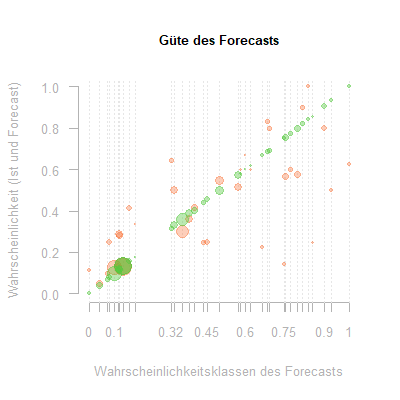
Um einen schnellen Eindruck von der Güte und den Schwächen des Verfahrens zu geben, stellen wir die Tabelle hier graphisch dar:

Auf der x-Achse befinden sich die Wahrscheinlichkeitsklassen, die die Bäume erzeugt haben. Ihnen wird auf der y-Achse grün ihre identische Forecastwahrscheinlichkeit und rot die in der entsprechenden Klasse gemessene Ist-Ausfallwahrscheinlichkeit zugewiesen. Die Größe der Punkte entspricht der Anzahl der Daten in der jeweiligen Klasse.

 

Auf jeder gestrichelten Linie befinden sich somit ein roter und ein zugehöriger grüner Punkt gleicher Größe.  Ihr Abstand auf der y-Achse repräsentiert den Fehler. Es zeigt sich, dass insbesondere kleine Klassen gänzlich fehlerhaft prognostiziert wurden. Der Baum ist somit bei der Erzeugung dieser Klassen bereits überoptimiert und sollte vorher abgebrochen werden.

Zufallswälder

Weiteren Aufschluss kann auch eine Analyse der Unterschiede zwischen den Bäumen geben, die auf Basis unterschiedlicher Trainingsdaten generiert wurden. Die generierten Bäume wie auch das genaue Testergebnis hängen von der Aufteilung der Daten in drei Teilmengen ab. Der Abhängigkeit von der jeweils gewählten Teilmenge wird bei den sogenannten Random Forests genauer nachgegangen.

1. Methode der Random Forests

Statt einen einzelnen Baum auf Basis eines Trainingsdatensatzes zu erzeugen, werden aus dem vorhandenen Datensatz eine Vielzahl zufälliger Teildatensätze erzeugt. Auch die Auswahl des Parameters, für den eine Teilung des Datensatzes vorgenommen wird, erfolgt zufällig:

• aus dem zur Verfügung stehenden Datensatz der Größe n werden m Teildatensätze dergleichen Größe erzeugt, indem aus dem Originaldatensatz n mal mit Zurücklegen gezogen wird.
• für jeden Teildatensatz wird ein Baum erzeugt
• dabei werden an jedem Knoten aus k Parametern zufällig Wurzel(k) Parameter ausgewählt
• nur von dieser Teilmenge der Parameter wird der für die nächste Teilung optimale Parameter nach obigem Algorithmus ausgewählt

Es entstehen auf diese Weise sehr viele leicht abweichende Bäume. Sie gleichen sich in Strukturen, die durch viele Daten belegt sind. Strukturen, die nur durch wenige Daten belegt sind, sehen in anderen Bäumen jeweils unterschiedlich aus.

 

Der Forecast aus einem solchen Random Forest Modell ergibt sich als der Mittelwert der Forecasts aller enthaltenen Bäume. Soll eine feste Zuordnung zu einer Klasse – keine Wahrscheinlichkeitszuweisung – Ergebnis des Forecasts sein, so wird als Forecast die Klasse bestimmt, der der Datensatz von den meisten Bäumen zugewiesen wird.

2. Gütetest

Wie vorher beschrieben, kann ein Gütetest mit einem vorher beiseite gesetzten Testdatensatz erfolgen. Dies reduziert jedoch die für die Kalibrierung verfügbaren Daten. Weiterhin werden bei jeder Baumerzeugung mittels Random Forests bereits von vornherein Daten beiseite gesetzt. Somit ist es naheliegend, jeden Baum des Zufallswaldes erst einmal gegen die Daten zu testen, die in seinen Kalibrierungsdaten jeweils nicht enthalten sind.

 

Als Testalgorithmus ergibt sich somit:

• für jeden Datensatz wähle alle die Bäume, in deren Kalibrierungsdaten der Datensatz nicht enthalten ist
• vergleiche die tatsächliche Kategorie dieses Datensatzes mit dem Durchschnitt (bzw. der Mehrheit) der Vorhersagen dieser Bäume

Als Gütemaß ist entweder der Prozentsatz der korrekt klassifizierten Daten oder die Summe der quadratischen Abweichungen zwischen Prognose und Ist sinnvoll.

Fazit

Einfache Klassifikationsbäume liefern ein intuitives, transparentes, sofort verständliches Ergebnis. Der Algorithmus ähnelt stark dem menschlichen Verhalten bei einer Entscheidungsfindung. Dies führt im Allgemeinen zu hoher Akzeptanz. Die im Nachhinein offenliegenden Entscheidungsregeln erlauben eine Einsicht in die zugrundeliegenden Daten. Klassifikationsbäume sind somit eine Datenanalyse- und Datamining-Technik.

 

Im Vergleich zu anderen klassischen Verfahren wie Regressionsverfahren und Diskriminanzanalyse können Klassifikationsbäume bis zu einem gewissen Punkt mit nichtlinearen Zusammenhängen und komplexen Interdependenzen zwischen den Ausgangsvariablen umgehen. Eine Stärke gegenüber anderen klassischen Verfahren ist weiterhin, dass sowohl kontinuierliche als auch diskrete Variablen als Ausgangsgrößen verwendet werden können. Allerdings können leicht komplexe und überangepasste Bäume entstehen, wenn der Algorithmus keinen einfachen Zusammenhang findet. Der Algorithmus garantiert zudem nicht, dass der gefundene Baum optimal ist.

 

In ihrer Weiterentwicklung als Random Forests gehören Klassifikationsbäume zusammen mit Neuronalen Netzen, Support Vector Machines, Selbstorganisierenden Karten und anderen Verfahren zu den Techniken des Machine Learnings.