Der Smart-Meter-Rollout wird in Kürze Ist-Lastzeitreihen für nahezu alle Kunden zur Verfügung stellen. Im gleichen Zuge steigen die Handlungsmöglichkeiten im Energievertrieb, die Prognosegüte zu verbessern und verbrauchsspezifische Preise und Tarife zu stellen. Clusteranalysen sind mathematische Verfahren zur Klasterung von Lastgängen eines Absatzportfolios. Dabei können sowohl ähnliche Verläufe innerhalb einer Zeitreihe (Typtage) wie auch Ähnlichkeiten zwischen Lastgängen (Kunden mit ähnlichem Verbrauchsmuster) gesucht werden.
Lastprognosen im Lichte von Smart Meter
Das Lastverhalten von Kunden- und Kundengruppen richtig zu prognostizieren und richtig zu bepreisen, ist bestimmend für die Wirtschaftlichkeit des Energievertriebs. Es ist somit eine der Kernaufgaben und notgedrungen auch der Kernkompetenzen der Energiewirtschaft.
Bislang wurde dem Energievertrieb diese Aufgabe im Massenkundengeschäft durch verbindliche Standardlastprofile stark erleichtert. Durch Smart Metering werden in Kürze Ist-Lastzeitreihen für nahezu alle Kunden zur Verfügung stehen. Auch eine Anpassung der Bilanzierungsregeln ist auf dem Weg. Hiermit bieten sich für Lastprognose und Bepreisung im Massengeschäft völlig neue Voraussetzungen.
Nichtsdestoweniger können die arbeitsintensiven Verfahrensweisen des Großkundengeschäfts nicht eins zu eins auf das Massengeschäft übertragen werden. Einzelprognosen und Einzelanalysen von Lastgängen sind im Massengeschäft nicht wirtschaftlich. Segmentierungen des Lastverhaltens in geeignete Kundenklaster werden erforderlich sein.
Die Gruppierung des Kundenportfolios nach typischem Lastverhalten in Verbindung mit geeignet erhobenen mit dem Lastverhalten korrespondierenden Kundeneigenschaften kann zudem einen entscheidenden Informationsgewinn für den Vertrieb darstellen und ist Basis für die Tarifentwicklung.
Der Vertrieb steht somit vor den Aufgaben:
- Lastprofile seines Absatzportfolios nach Ähnlichkeit zu klastern und typischen Profilen zuzuordnen
- vertrieblich ermittelbare Kriterien zu eruieren, aus denen die Klasterzugehörigkeit / das typische Lastverhalten abgeleitet werden kann
Der vorliegende Artikel beschäftigt sich mit dem ersten Teil der Aufgabe.
Methodisches Vorgehen bei einer Clusteranalyse
Die Clusteranalyse bietet die Möglichkeit, eine Zeitreihen in „Schubladen“ mit ähnlichem Verlauf zu sortieren, ohne dabei inhaltliche a priori-Annahmen zu treffen. Somit können mit einer Clusteranalyse:
- Lastgänge eines Portfolios in Cluster sortiert werden, die jeweils Lastgänge ähnlicher Struktur enthalten
- Tagesverläufe eines Lastgangs oder einer Preiszeitreihe in Klassen mit ähnlichem Verlauf sortiert werden (sogenannte Typtage)
Es gibt viele Verfahren zur Clusteranalyse. In diesem Artikel konzentrieren wir uns auf klassische sogenannte hierarchische Verfahren. Die Ähnlichkeitssuche mit einem solchen Verfahren erfordert im Allgemeinen mehrere Schritte:
- Zunächst werden meist über eine geeignete Normierung und Bereinigung Effekte eliminiert, die im Rahmen der Clusteranalyse als nicht relevant erachtet werden, aber zu einer Klassifizierung von Lastgängen als unterschiedlich führen würden.
- In einem zweiten Schritt wird auf den normierten Zeitreihen eine Distanzfunktion definiert, mit deren Hilfe bestimmt werden kann, welche Zeitreihen nahe beieinander liegen (also ähnlich sind) und welche nicht.
- In einem iterativen Verfahren werden nun nahe beieinanderliegende Zeitreihen herausgefiltert und Cluster („Anhäufungen“) von Zeitreihen identifiziert
Einige Clusterverfahren ermöglichen eine freie Wahl der Distanzfunktion. Übliche solche Funktionen stellen wir in einem folgenden Kapitel kurz vor.
Die Anzahl der gewünschten Cluster kann vorab gesetzt oder durch Zielfunktionen ermittelt werden. Ziel ist dabei nach Möglichkeit systematisch unterschiedliche Zeitreihen zu separieren und „zufällige“ Abweichungen bei der Clusterung zu ignorieren. Das bedeutet, dass der Abbruch optimalerweise an einer Stelle erfolgt, wo eine weitere Zusammenführung von Clustern zu einem großen Anwachsen der Distanzen innerhalb des Clusters führt.
Bereinigung und Normierung der Zeitreihen
Um Zeitreihen sinnvoll vergleichen zu können, werden oftmals für die Untersuchung nicht relevante Unterschiede vorab bereinigt. Teilweise werden die Zeitreihen auch vorher geeignet vereinfacht, um eine bessere Rechenzeit und ein stabileres Ergebnis auf großen Datenmengen zu erreichen.
1. Fehlwerte und Ausreißer
Zunächst einmal ist es sinnvoll, Ausreißer und Fehldaten in historischen Zeitreihen mit Ersatzwertverfahren zu bereinigen, da sie zur Verfälschung der Ergebnisse führen können.
2. Normierung auf gleiche Gesamtarbeit
In der Energiewirtschaft ist es weiterhin oft sinnvoll, zu vergleichende Zeitreihen auf gleichen Jahresabsatz zu normieren. Das heißt, statt einer stündlichen Zeitreihen (zi)i betrachtet man die entsprechende normierte Zeitreihe (zNi)i mit
Diese Normierung auf Jahresabsatz 1 erfolgt wenn zweckmäßig zuletzt, nachdem alle anderen unerwünschten Effekte bereinigt wurden.
3. Trendbereinigung
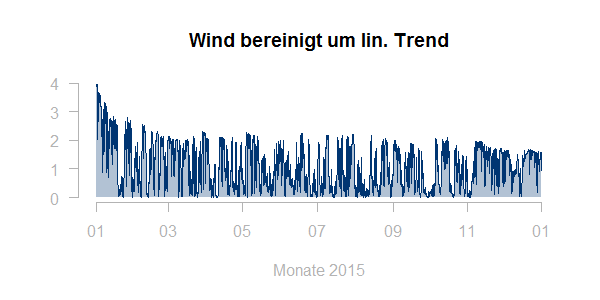
Auch Trends in den Daten sollte man möglicherweise bereinigen. Hier zum Beispiel ein Windeinspeiselastgang mit deutlichen Zubaueffekten:
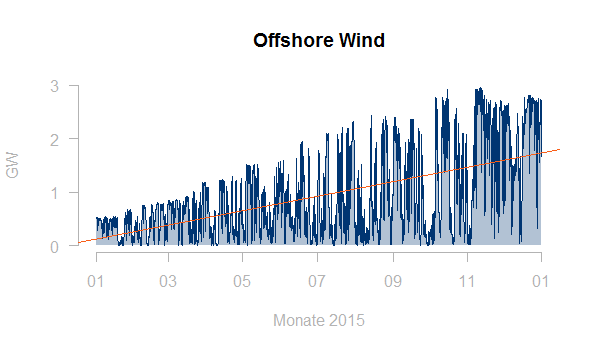
Typischerweise wäre man eher an einem typischen Profil für eine konstante installierte Leistung interessiert. Eine erste Idee zur Bereinigung ist, die Zeitreihe durch den linearen Trend (rote Linie in obiger Graphik) zu teilen. Allerdings führt dies nicht zu einem befriedigenden Ergebnis:
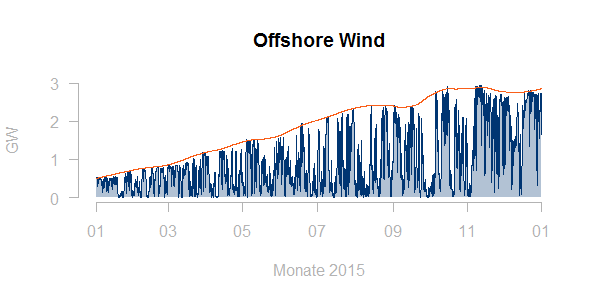
Möchte man keine weiteren Daten hinzuziehen, so lässt sich die verfügbare Leistung zum jeweiligen Zeitpunkt gut als ein gleitendes Maximum (etwas geglättet) darstellen:
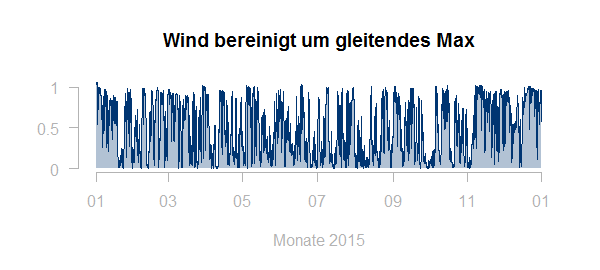
Normierung der Zeitreihe mit diesem gleitenden Maximum ergibt ein befriedigendes Ergebnis:
4. Zufällige „Störungen“ des Lastverhaltens
Klassische Methoden der Clusteranalyse liefern kein sinnvolles und stabiles Ergebnis, wenn die systematischen Strukturen, die man zu finden hofft, stark von zufälligen Effekten überlagert werden. Beispielhaft für dieses Problem zeigen wir weiter unten eine Clusteranalyse der Spotpreise.
Daher ist es zweckmäßig, bei der Analyse eines Kundenportfolios die zu untersuchenden Lastgänge nach Möglichkeit von vornherein auf ihre systematische Struktur zu reduzieren. Hierzu kann man für jeden Lastgang die folgenden reduzierten Datensätze betrachten:
- die typische Woche aus durchschnittlichem Montags-, Dienstags-, …, Sonntags-Lastverlauf
- ein für diesen Lastgang generiertes Quasi-Standardlastprofil
Für ein solches Quasi-Standardlastprofil werden Typtage (z.B. Mo, Di-Do, Fr, Sa, Sonn- und Feiertag) und Saisons definiert (z.B. Sommer, Winter, Übergangszeit). Für jede Kombination aus Typtag und Saison erhält man einen typischen Verlauf durch Mittlung der Verläufe aller Tage, die in diesen Typtag und diese Saison fallen.
5. Anforderungen an die Normierung
Die Normierung dient zweckmäßigerweise auch der Vereinfachung der Daten und erhöht somit die Performance der Clusteralgorithmen. Sie darf jedoch keine Effekte bereinigen, die in Wirklichkeit kostenbestimmend sind und somit gerade herausgefiltert werden sollen.
Vielfach werden in Clusteranalysen beispielsweise Abstandsmaße definiert, die Zeitreihen als gleich klassifizieren, die sich nur durch eine zeitliche Verschiebung unterscheiden. Dies ist für die Energiewirtschaft nicht zweckmäßig, da gerade die zeitliche Verteilung der Last (Maximallast nachts oder tagsüber, werktags oder am Wochenende) entscheidend und kostenbestimmend ist.
Definition von Distanzmaßen
Eine Zeitreihe der Länge n wird als ein Punkt im Rn interpretiert. Eine stündliche Zeitreihe über ein Jahr entspricht dann beispielsweise einem Punkt im R8760. Ein Distanzmaß für Zeitreihen einer vorgegebenen Länge n ist somit ein Distanzmaß (oder eine Distanzfunktion) des Rn. Hierfür gibt es mehrere naheliegende Möglichkeiten:
Ein erstes naheliegendes Distanzmaß ist die euklidische Metrik. Der Abstand zwischen zwei Zeitreihen p, q der Länge n (entspricht zwei Punkten im Rn) ist dann:
Eine Verallgemeinerung hiervon sind die sogenannten Minkowski-Metriken oder Minkowski-Distanzen, die für jedes feste k ≥ 1 wie folgt definiert sind:
Ein sinnvolles Maß für die Ähnlichkeit von Zeitreihen ist offensichtlich auch ihre Korrelation. Der empirische Korrelationskoeffizient für zwei Zeitreihen p, q ergibt sich als
wobei
und
ist.
Die Idee ist nun, dass hoch korrelierte Zeitreihen einen kleinen Abstand haben und niedrig korrelierte einen großen. Explizit soll der Abstand von zwei Zeitreihen mit Korrelation 1 gleich 0 sein und der Abstand von zwei Zeitreihen mit Korrelation -1 soll maximal unter allen möglichen Abständen sein. Ein mögliches Distanzmaß mit diesen Anforderungen ist:
Hiermit ist dann also
.
Die Distanz kann hier als Winkel interpretiert werden, nämlich als Winkel zwischen den durch die Punkte
und
definierten Ursprungsvektoren des Rn.
Eine einfachere Variante für ein Distanzmaß mit den genannten Anforderungen ist:
Wir verwenden im Folgenden als Distanzmaß die euklidische Metrik.
Hierarchische Clusterbildung mit Fusionierungsalgorithmen
Es gibt verschiedene Verfahren, aus betrachteten (Teil-)Zeitreihen Cluster zu bilden. Verbreitet sind außer den hier diskutierten hierarchischen Verfahren z.B. auch der k-Means-Algorithmus. Ein Vorteil der hierarchischen Verfahren ist, dass sie eine freie Wahl der Metrik ermöglichen. Es wird unterschieden zwischen:
- divisiven Clusterverfahren, in denen zunächst alle Objekte als zu einem Cluster gehörig betrachtet und dann schrittweise die bereits gebildeten Cluster in immer kleinere Cluster aufgeteilt werden, bis jeder Cluster nur noch aus einem Objekt besteht
- agglomerativen Clusterverfahren, in denen zunächst jedes Objekt einen Cluster bildet und dann schrittweise die bereits gebildeten Cluster zu immer größeren zusammengefasst werden, bis alle Objekte zu einem Cluster gehören
Agglomerative hierarchische Clusterverfahren haben die größte Verbreitung. Sie starten mit dem Zustand, dass jedes Objekt (jeder Lastgang) sein eigenes Cluster ist. Schrittweise werden immer die Cluster mit der kleinsten Distanz zueinander zusammengeführt, bis alle Cluster vereinigt sind. Die optimale Anzahl von Clustern wird innerhalb des Prozesses dann über ein sinnvolles Abbruchskriterium bestimmt. Hierzu dient unter anderem das sogenannte Dendrogram.
Für die Messung der Distanz zwischen Clustern und das daraus abgeleitete Fusionskriterium gibt es unterschiedliche Möglichkeiten. Einige davon stellen wir im Folgenden vor.
1. Single Linkage
Beim Single-Linkage ist die Distanz zwischen zwei Clustern A und B der Abstand zwischen den beiden Objekten a, b der beiden Cluster, die den geringsten Abstand voneinander haben:
2. Complete Linkage
Beim Complete-Linkage ist die Distanz zwischen zwei Clustern A und B der Abstand zwischen den beiden Objekten a, b der beiden Cluster, die den größten Abstand voneinander haben:
3. Average Linkage
Beim Average Linkage wird der Mittelwert der Distanzen aller Verbindungen von A nach B gebildet:
Dabei sind
die Anzahl der Objekte in A und B
4. Centroid – Method
Bei der Centroid- Method wird der Abstand der Zentren der beiden Gruppen gemessen:
Dabei sind
die Schwerpunkte der beiden Cluster bezogen auf die Metrik.
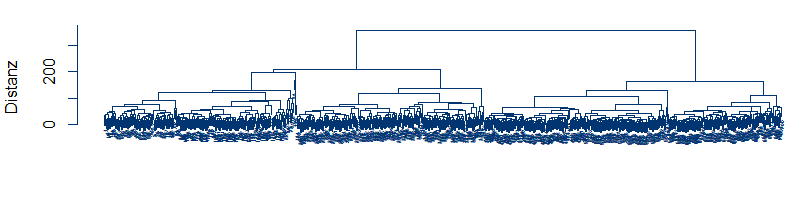
Auswertung mit dem Dendrogramm
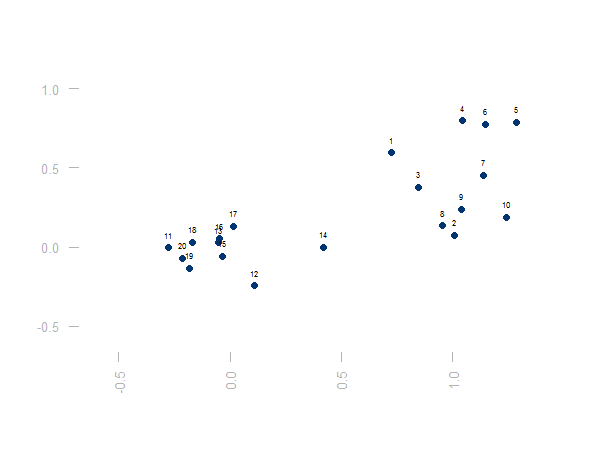
Der Algorithmus der Clusterbildung startet nun mit dem Zustand, dass jedes Objekt / jede Zeitreihe ihr eigenes Cluster bildet:
Dann werden in jedem Schritt die beiden Cluster fusioniert, die nach dem gewählten Fusionierungsalgorithmus (siehe oben) die geringste Distanz voneinander haben. Dies kann man solange fortsetzen, bis alle Objekte in einem Cluster sind. Die sukzessive Clusterfusion und die immer größeren Distanzen zwischen fusionierten Clustern lassen sich in einem Dendrogramm darstellen:
Auf der y-Achse ist die Distanz der zusammengeführten Cluster abgebildet. Auf der x-Achse sind die Ausgangsobjekte. Die Joche, die unterschiedliche Cluster verbinden, befinden sich jeweils auf der Höhe der Cluster-Distanz. Man sieht, dass die Cluster zunächst sehr nahe beieinander liegen. Am Ende werden zwei weit voneinander entfernte Cluster verbunden. Eine gute Abbruchstelle liegt an einer Stelle, mit langen senkrechten Achsen. Hier vergrößert sich der Abstand massiv, bevor eine weitere Fusion von Clustern möglich wird.
Wie ein Blick auf die ursprüngliche Punktegraphik nahelegt, lässt sich die Punktwolke gut durch zwei Cluster beschreiben.
Wie erfolgt nun die Anwendung auf Kundenportfolien?
Die Durchführung einer solchen Clusteranalyse auf einer geeignet normierten Datenbasis von Lastgängen ist sehr einfach. Die gängigen Verfahren:
- agglomerative und divisive hierarchische Verfahren
- k-Means
- Density-Methoden
- usw.
sind in den üblichen Statistik-Softwarepaketen (Matlab, R …) mit vielen Varianten und auch unterschiedlichen Metriken implementiert.
Betrachtet man z.B. den historischen Verlauf der Spotpreise über die Jahre 2015-2016 als Tabelle mit Tagen als Zeilen und Stunden als Spalten, so erhält man eine Clusterung der Tagesverläufe mit einem agglomerativen, hierarchischen Verfahren bei R über die zwei Zeilen:
library(cluster)
p1 ← agnes(spotpreise, metric = „euclidean“, stand = FALSE, method = „average“)
Einen Dendrogramm-Plot erhält man über die weitere Zeile:
plot(p1)
Hier ist er:
Mit wenigen Zeilen lassen sich die in jedem Cluster enthaltenen Datensätze auswerten. Allerdings erhält man dabei – wie bereits in obigem Abschnitt zu stochastischen Störungen erwähnt – nicht unbedingt ein brauchbares Ergebnis. Dies zeigt sich schon bei der Anzahl der Elemente pro Cluster
groups.2 = cutree(p1,2) ## erste 2 Cluster
table(groups.2) ## Anzahl Elemente anzeigen
Antwort:
groups.2
1 2
717 14
Für 20 Gruppen sieht die Gruppenverteilung wie folgt aus:
groups.20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
22 2 6 446 104 2 7 33 86 2 2 1 2 1 5 4 1 3 1 1
Ein agglomeratives Verfahren findet bei solchen Daten auf jeder Stufe Ausreißer, die in eigene Klassen aussortiert werden und sortiert den Rest im Wesentlichen in Rest. Bei einem divisiven Verfahren sieht das Dendrogramm auf ersten Blick besser aus, es entstehen jedoch trotzdem keine sinnvollen Klassen.
Fazit und Ausblick
Wie bereits oben erwähnt, sind Zeitreihen mit hohem stochastischen Anteil für eine Analyse mit klassischen Clusterverfahren nicht geeignet. Somit sind bei den beschriebenen klassischen Verfahren die vorgelagerten Schritten zur Normierung und Vereinfachung von entscheidender Bedeutung. Auch Überlegungen zur Wahl des Clusterverfahrens und die Wahl der Metrik sind wichtig, um ein aussagekräftiges Ergebnis zu erhalten.
Ein gegenüber stochastischen Störungen robusteres Verfahren sind die sogenannten selbstorganisierenden Karten. Sie beruhen auf ähnlichen geometrischen Ideen, sind aber ein iterativer und selbstlernender Algorithmus der dem Machine-Learning zuzurechnen ist. Selbstorganisierende Karten verhalten sich gegenüber Störungen und Datenfehlern relativ robust. Auch dieser Algorithmus ist in mathematischer Software verfügbar und möglicherweise ebenfalls einmal einen Artikel wert.
Um tatsächlich Kunden Clustern zuzuordnen und Produkte Cluster-abhängig zu gestalten, sind weiterhin Kundeninformationen erforderlich, die möglichst von vornherein zum Zeitpunkt des Vertragsabschlusses oder bereits für die Kundenansprache eine Clusterzuordnung ermöglichen. Aus einer stichprobenbasierte Erhebung von Kundendaten z.B. über Umfragen in Kombination mit einer Clusteranalyse des Lastverhaltens kann ermittelt werden, welche Kundeneigenschaften tatsächlich das Lastverhalten prägen.