Wie ermittelt man den mengen- oder wertneutralen Hegde in Base und Peakkontrakten für einen Strom- oder Gasfahrplan und welches Verfahren ist richtiger? Energieversorger liefern ihren physisch belieferten Kunden ihren Energiebedarf in jeder Viertelstunde und stellen hierfür auch im Vorhinein einen Preis. Für die Absicherung am Terminmarkt stehen jedoch nur Standardprodukte zur Verfügung.
Handelbare Terminprodukte
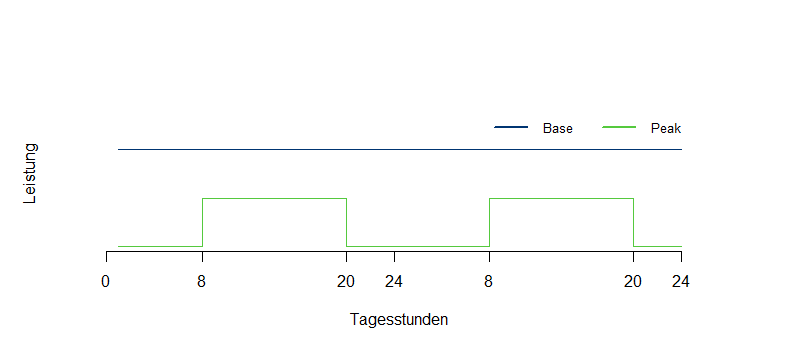
Die handelbaren Terminkontrakte im Strommarkt sind im Wesentlichen Jahres-, Quartals- und Monatskontrakte Base und Peak. Der Basekontrakt besteht in einer Bandlieferung mit gleicher Leistung über alle Viertelstunden des Lieferzeitraums. Der Peakkontakt besteht in einer Bandlieferung Mo – Fr von 8:00 – 20:00 Uhr. Nicht-Peakzeiten werden auch als Offpeakzeiten bezeichnet. Eine Bandlieferung zu Offpeakzeiten, die sich als Differenz aus einer Baselieferung und einer Peaklieferung mit gleicher Leistung ergibt, heißt auch Offpeakkontrakt.
Im Gasmarkt werden ausschließlich Baselieferungen für die Lieferzeiträume Jahr, Quartal und Monat und zusätzlich die Saisonkontrakte Sommer und Winter gehandelt. Eine Season beinhaltet entweder jeweils die Monate Oktober bis März (Winter-Season) oder jeweils die Monate April bis September (Sommer-Season).
Dies sind nicht alle Kontrakte, die an den Terminmärkten handelbar sind. Weitere Kontrakte an der EEX und auf OTC-Märkten (sogenannte Offstandards) werden jedoch wegen der vergleichsweise geringeren Liquidität hier zunächst nicht betrachtet.
Auch die genannten Kontrakte sind immer nur für einen begrenzten Zeitraum in die Zukunft liquide handelbar. Darüber hinaus werden zwar auf den OTC-Märkten ebenfalls Preise gestellt. Diese enthalten dann aber möglicherweise Sicherheitsaufschläge des Lieferanten. Jahreskontrakte können im allgemeinen für die drei Folgejahre liquide gehandelt werden, Quartalskontrakte bis zu 6 Quartale in die Zukunft, Monatskontrakte bis zu 6 Monate in die Zukunft. Dies ist aber immer auch von den Marktzugängen des Unternehmens (Anzahl der EFET-Verträge, vorhandener Börsenzugang) und der aktuellen Marktsituation abhängig. Die handelbaren Größe beträgt in der Regel 1 MW. Der Preis wird auf 0,01 €/MWh genau quotiert.
Wir betrachten im Folgenden die Ermittlung eines optimalen Hedges für einen Stromfahrplan in Terminkontrakten Base und Peak. Für einen Gasfahrplan lässt sich ein optimaler Hedge ähnlich ermitteln. Dort erfolgt eine Absicherung nur mit Basekontrakten.
Mengenneutraler Hedge
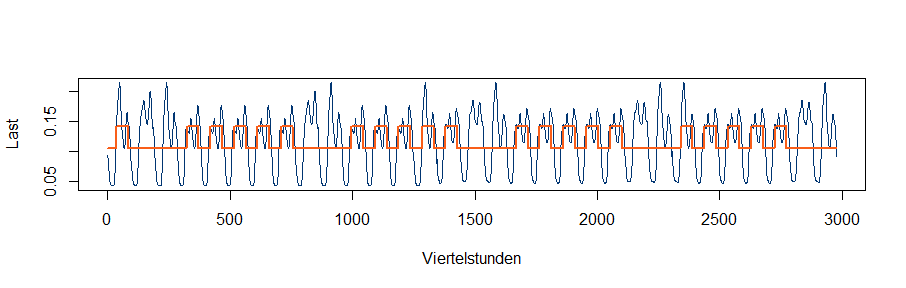
Um eine Vertriebslieferung in Viertelstundengranularität auf den Energiehandelsmärkten abzusichern, muss der Lieferfahrplan somit bestmöglich in Handelskontrakten approximiert werden. Die erste Frage ist dabei, welche Handelskontrakte im Augenblick überhaupt handelbar sind. Je nachdem muss die Absicherung in Jahreskontrakten, Quartalskontrakten oder Monatskontrakten erfolgen.
Der einfachste Ansatz die erforderlichen Hedgekontrakte zu ermitteln, ist der mengenneutrale Hedge. Der mengenneutrale Hedge enthält im jeweiligen Hedgezeitraum (Jahr, Quartal oder Monat) dieselbe Lieferungsmenge wie der ursprüngliche Lastgang. Die Mengengleichheit gilt auch jeweils separat betrachtet für Peak- und Offpeakzeiten.
Bei der Berechnung des mengenneutralen Hedges für einen Lastgang L (exemplarisch für Jahreskontrakte) ergibt sich die erforderliche
- Jahresbaseleistung B als Mittelwert über die Leistung Li aller Offpeak-Stunden des Lieferzeitraums
- Jahrespeakleistung P als Mittelwert über die Leistung Li aller Peak-Stunden des Lieferzeitraums abzüglich der bereits ermittelten Baseleistung
Soll ein Hedge in Quartals- oder Monatskontrakten erfolgen, so wird der Fahrplan in Quartals- oder Monatslieferungen zerlegt und für jeden dieser Einzelfahrpläne obige Rechnung durchgeführt. Es ergibt sich jeweils die Base-Peak-Zerlegung für jeden Monat oder jedes Quartal.
Wertneutraler Hedge
Im Gegensatz zum mengenneutralen Hedge hat der wertneutrale Hedge im jeweiligen Hedgezeitraum (Jahr, Quartal oder Monat) nicht dieselbe Menge wie der ursprüngliche Lastgang sondern denselben Wert. Auch diese Gleichung soll wieder separat für Peak- und Offpeakzeiten gelten. Auch hier kann ein Hedge je nach Verfügbarkeit liquider Terminkontrakte auf Jahres-, Quartals- oder Monatsbasis erfolgen.
Bei der Berechnung des wertneutralen Hedges für einen Lastgang L (exemplarisch für Jahreskontrakte) ergibt sich die erforderliche
- Jahresbaseleistung B als gewichtetes Mittel über die Leistung Li aller Offpeak-Stunden des Lieferzeitraums gewichtet mit der aktuellen HPFC H
- Jahrespeakleistung P als gewichtetes Mittel über die Leistung Li aller Peak-Stunden des Lieferzeitraums gewichtet mit der aktuellen HPFC H abzüglich der bereits ermittelten Baseleistung
Vergleich mengenneutraler und wertneutraler Hedge
Bei einem mengenneutralen Hedge hat der Differenzfahrplan zwischen Fahrplan und Hedge die Gesamtmenge Null. Wird im Unternehmen grundsätzlich mengenneutral gehedgt, so ist zu erwarten, dass beim Schließen des Differenzfahrplans auf dem Spotmarkt ebenso viel gekauft wie verkauft wird.
Bei einem wertneutralen Hedge hat der Differenzfahrplan zwischen Fahrplan und Hedge den Wert Null. Die Erwartung ist hier, dass das Schließen des Differenzfahrplans auf dem Spotmarkt nicht systematisch zu Ergebnissen in einer Richtung (Aufwand oder Erlöse) führen wird. Bei einem typischen Vertriebslastgangs führt es mengenmäßig dazu, dass mehr Menge gekauft wird, als im Fahrplan geliefert wird und somit netto Mengen auf dem Spotmarkt verkauft werden.
Die eigentliche Erwartung an eine Terminmarktabsicherung ist jedoch, dass das Hegdegeschäft den Preis, der für die Fahrplanlieferung gestellt wurde, bestmöglich absichert. Wir nehmen somit an, dass zum gleichen Zeitpunkt ein Lastgang L an einen Kunden verkauft wurde und für dieses Geschäft ein Hedge am Terminmarkt AL getätigt wurde. Ist H0 die HPFC zum Abschlusszeitpunkt, so haben Lastgang und Hedge gemeinsam den Wert:
Dabei ist
das Skalarprodukt von Vektoren, d.h. von Zahlenfolgen x = (x1, … , xn) und y = (y1, … , yn). Die Frage ist nun, wie weit der Hedge das Unternehmen gegen Marktpreisänderungen absichert. Ein geändertes Marktniveau zu einem späteren Zeitpunkt spiegelt sich in einer HPFC H1 wieder. Die betrachteten Geschäfte haben nun den Wert:
Das Ergebnis aus der Marktpreisänderung ergibt sich für das Unternehmen als
Nun kann man zwei Spezialfälle betrachten:
1. Preisshift um eine Konstante
Wenn der neue Marktpreis H1 sich als H0 plus einen konstanten Aufschlag a (positiv oder negativ) auf alle HPFC-Stundenpreise ergibt, so ist die Ergebniswirkung daraus:
Dabei istI ein Vektor mit nur Einsen und i läuft über alle Werte des indizierten Vektors. Für einen mengenneutralen Hedge ist die Menge des Differenzfahrplans AL – L Null, das Ergebnis ist somit Null und der Hedge perfekt. Mengenneutrale Hedges sichern perfekt gegen Parallelshifts des Preisniveaus.
2. Proportionale Preisveränderung
Ein anderer naheliegender Spezialfall ist, dass der neue HPFC-Preis H1 sich durch eine proportionale Anpassung der alten HPFC ergibt, d.h. alle Preise haben sich um einen konstanten Faktor geändert und H1 = a · H0. Dann ist die Ergebniswirkung daraus:
Für einen wertneutralen Hedge ist
Das Ergebnis ist somit Null und der Hedge perfekt. Wertneutrale Hedges sichern perfekt gegen proportionale Preisänderungen.
Was ist richtiger?
Tatsächlich ändern sich am Terminmarkt die Preise einiger Kontrakte. Die Änderungen lassen sich im allgemeinen weder durch eine additive (Parallelshift) noch durch eine multiplikative (proportionale) Anpassung der HPFC vollständig abbilden. Ob jedoch eine generelle Änderung des Preisniveaus am Terminmarkt eher in einer proportionalen Anpassung von Stundenpreisen der HPFC umgesetzt wird oder eher in Parallelshifts der HPFC, wird durch das verwendete HPFC-Modell vorgegeben. Die meisten HPFC-Modelle reagieren auf eine Änderung der handelbaren Terminpreise überwiegend mit einer proportionalen Anpassung der HPFC-Stundenpreise. Insofern zeigen wertneutrale Hedges für ein HPFC-bewertetes Portfolio eine bessere Absicherungswirkung als mengenneutrale Hedges.
 Im Energiehandel, im Vertrieb, in vielen Bereichen der Energiewirtschaft kommt man gut damit durch, das Netz als Kupferplatte und den Strom als ein Wertpapier zu betrachten, das virtuell gehandelt wird. Erzeugung und Netzbetreiber wissen, dass es nicht so ist. Im Folgenden ein paar Grundlagen zum Rechnen mit [...]
Im Energiehandel, im Vertrieb, in vielen Bereichen der Energiewirtschaft kommt man gut damit durch, das Netz als Kupferplatte und den Strom als ein Wertpapier zu betrachten, das virtuell gehandelt wird. Erzeugung und Netzbetreiber wissen, dass es nicht so ist. Im Folgenden ein paar Grundlagen zum Rechnen mit [...]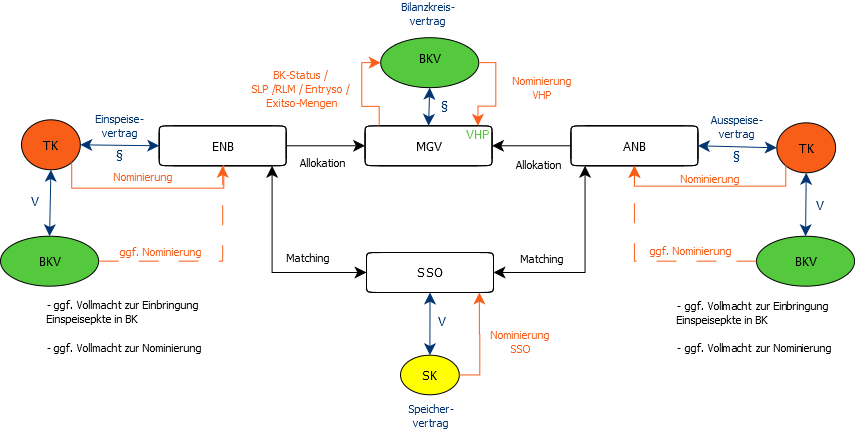 Bilanzkreismanagements Gas ist ein komplexes Thema. Das zeigt die Vielzahl relevanter Vorgaben und Veröffentlichungen und der bloße Umfang des Geode Leitfadens Bilanzkreismanagement Gas, in dem die diesbezüglichen Prozesse verbindlich geregelt werden. Ziel dieses Artikels ist es, unter Nennung jeweils relevanter Vorgaben und Dokumente einen ersten Überblick zu geben.
Wir beschränken uns [...]
Bilanzkreismanagements Gas ist ein komplexes Thema. Das zeigt die Vielzahl relevanter Vorgaben und Veröffentlichungen und der bloße Umfang des Geode Leitfadens Bilanzkreismanagement Gas, in dem die diesbezüglichen Prozesse verbindlich geregelt werden. Ziel dieses Artikels ist es, unter Nennung jeweils relevanter Vorgaben und Dokumente einen ersten Überblick zu geben.
Wir beschränken uns [...]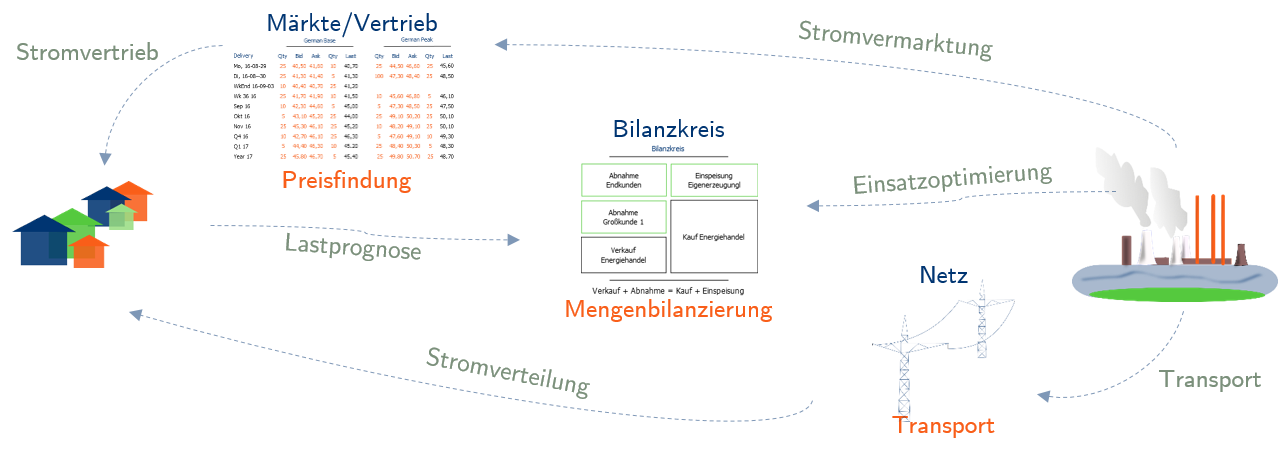 Die Novellierung des Energiewirtschaftsgesetzes von 1998 änderte die Rahmenbedingungen der Energiewirtschaft grundlegend. Im Folgenden werden die zentralen Mechanismen dieses lange als „Neue Welt der Energiewirtschaft“ bezeichneten Marktdesigns dargestellt.
Ziel und Herausforderung des 1998 in seinen Grundzügen geschaffenen und seither weiterentwickelten Marktdesigns ist es, einerseits durch Wettbewerb für [...]
Die Novellierung des Energiewirtschaftsgesetzes von 1998 änderte die Rahmenbedingungen der Energiewirtschaft grundlegend. Im Folgenden werden die zentralen Mechanismen dieses lange als „Neue Welt der Energiewirtschaft“ bezeichneten Marktdesigns dargestellt.
Ziel und Herausforderung des 1998 in seinen Grundzügen geschaffenen und seither weiterentwickelten Marktdesigns ist es, einerseits durch Wettbewerb für [...]
3 Kommentare
Tim W. · 11. November 2016 um 10:07
Vielen Dank für diese spannende Seite. Ich habe viele gute Informationen gefunden.
Aber nun habe ich eine Frage: Ist es richtig, dass bei der Berechnung der Base Leistung tatsächlich die off-Peak Stunden verwendet werden? Müssten da nicht eigentlich alle Stunden berücksichtigt werden?
Vielen Dank und Grüße
Marianne Diem · 11. November 2016 um 11:40
Vielen Dank für das Feedback. Zu Ihrer Frage:
Wenn Sie nur mit Basekontrakten hedgen möchten, müssen Sie alle Stunden berücksichtigen.
Wenn Sie mit Base und Peakkontrakten hedgen möchten, ergibt sich die Leistung des erforderlichen Basekontraktes als mittlere Leistung der Offpeakstunden des Fahrplans. Hiermit sind dann im ersten Schritt die Offpeakzeiten des Fahrplans perfekt gehedgt, die Peakzeiten nicht.
Um im zweiten Schritt den Hedge zu Peakzeiten zu korrigieren, wird der Peakkontrakt genutzt. Die Leistung des benötigten Peakkontraktes ergibt sich als mittlere Leistung der Peakstunden des Fahrplans abzüglich der Leistung, die bereits über den vorher ermittelten Basekontrakt abgesichert ist. Gruß, Marianne Diem
Tim W. · 11. November 2016 um 15:14
Stimmt! jetzt wird es mir auch klar. Vielen Dank für die Erläuterung.