Marktrisikosteuerung mit VAR, Greeks & Co

Wie können Marktrisiken eines Portfolios gesteuert werden. Welche Bedeutung haben Sensitivitäten und die sogenannten Greeks. In welchem Zusammenhang stehen sie zur Wertentwicklung des Portfolios und zu Risikokennzahlen wie dem Value-at-Risk.

Zentraler Bestandteil des Risikomanagements ist die Kontrolle von Preisrisiken an den Energiemärkten. Gegenstand dieses Artikels sind Methoden und Kennzahlen zur Marktrisikosteuerung eines Portfolios.

Portfoliostrukturen

Basis der Marktrisikosteuerung ist die Zusammenführung von am Markt getätigten Handelsgeschäften und von physischen Positionen, die Marktrisiken unterliegen, in geeigneten Portfolien, siehe hierzu auch den Artikel zum Portfoliomanagement.

1. Das Portfolio als Bewertungsbasis

Ein Portfolio besteht aus marktrisikobehafteten Positionen und Werten, sogenannten Assets, hier insbesondere

Energiehandels- und -vertriebskontrakten
Physischen Assets wie z.B. dem Vertriebsabsatz oder Kraftwerken, Importverträgen oder Speichern

Für die enthaltenen Assets des gegebenen Portfolios soll Marktwert, physische Netto-Lieferposition und Risiko

zusammengefasst betrachtet werden
von einem zugewiesenen Portfoliomanager bewirtschaftet werden
einem definierten Geschäftsbereich zugeordnet werden.

Die Portfoliostruktur dient somit

der Dokumentation von Handelszwecken
der Zuweisung von Ergebnissen und Risiken zu Handelszwecken und Geschäftsbereichen und
zur Steuerung der physischen Lieferpositionen.

2. Anforderungen an die Portfoliodarstellung

Wir gehen weiterhin davon aus, dass die betrachteten Portfolien vollständig in einem Handelssystem erfasst sind. Hierzu müssen komplexe physische Assets wie Kraftwerke und Speicher als virtuelle Verträge in einer Form dargestellt werden, die den Marktwert und seine Abhängigkeit von Marktpreisänderungen sowie die sich je nach Marktpreisniveau ergebenden physischen Lieferpositionen ausreichend gut wiedergibt, um eine wirksame Ergebnis- und Risikosteuerung zu ermöglichen.

Die repräsentative Darstellung von Kraftwerken und Speichern im Handelssystem bemisst sich somit danach, dass

die erwartete Lieferposition in allen Commodities in Abhängigkeit vom Marktpreis korrekt dargestellt ist
der Marktwert des Assets ausreichend genau wiedergegeben ist
die Marktpreisabhängigkeit des Marktwertes ausreichend genau wiedergegeben ist

Dieselbe Erwartung wird an die Abbildung von Handelsgeschäften und anderen Assets gestellt. Wird sie erfüllt, ergibt sich der Marktwert M des Portfolios als Summe aller Marktwerte M_i der im Portfolio enthaltenen Assets:

$M_{\text{Portfolio}} = \sum_{i \in \text{Portfolio}} M_i$

Risiken aggregieren sich nicht ganz so einfach, hier kommt es auf Korrelationen an. Verhalten sich die Wertentwicklungen von zwei Assets gegenläufig, so ist das Gesamtrisiko geringer als die Summe der Einzelrisiken. Wie sich das Gesamtrisiko eines Portfolios ermitteln und steuern lässt, ist Gegenstand des Artikels.

Marktbewertung von Assets

Der tägliche Marktwert eines Portfolios ergibt sich somit wie wir gesehen haben als Summe der Marktwerte aller enthaltenen Assets. Somit müssen zur Portfoliobewertung alle enthaltenen Assets bewertet werden. Je nach Asset ist diese Aufgabe sehr unterschiedlich schwierig. Zum Teil – insbesondere bei physischen Assets – Realoptionen – ist sie nur näherungsweise möglich bzw. zweckmäßig.

1. Terminkontrakte

Am einfachsten ist die Marktbewertung bei den Standardkontrakten Base und Peak des Terminmarktes Gas, Strom (oder auch Öl), bei denen ein festes Lieferprofil auf Termin verkauft oder gekauft wird. Der aktuelle Marktwert M des Kontraktes ergibt sich hier als:

$M = (m - k) \cdot L$

wobei
L die Liefermenge in MWh (positiv bei Kauf, negativ bei Verkauf)
m der aktuelle Marktpreis des Standardkontrakts in €/MWh
k der kontrahierte Preis des Kontrakts in €/MWh

2. Vertriebskontrakte mit marktpreisunabhängiger Absatzmenge

Vertriebsverträge beschränken sich nur selten auf die Lieferung eines fixen Lieferprofils. Insbesondere beim Absatz an kleinere Kunden und im Endkundenmarkt kann der Kunde zu einem festen Preis soviel Strom und Gas ziehen, wie er benötigt. Allerdings wird im Allgemeinen in diesem Marktsegment nicht davon ausgegangen, dass der Bezug des Kontrahenten vom Marktpreis abhängt. D.h. der Absatz erhöht sich nicht, wenn der Strom- oder Gaspreis teurer ist. Vor diesem Hintergrund wird in der Regel die Absatzprognose zwar regelmäßig aktualisiert. Auf Basis einer aktuellen Absatzprognose P ergibt sich der Marktwert der Absatzposition aber wie oben als:

$M = (m - k) \cdot P$

wobei
P die aktuelle Absatzprognose als 1/4h- Fahrplan in MWh (positiv bei Kauf, negativ bei Verkauf)
m die aktuelle Marktbewertung der Absatzprognose in €/MWh mittels einer HPFC
k der kontrahierte Preis in €/MWh

3. Marktpreiskorrelierte Vertriebskontrakte

Der Gasabsatz an Endkunden ist typischerweise temperaturabhängig. Das heißt die Absatzprognose P ist eine Funktion der Temperatur t. Einerseits kann sich hieraus indirekt doch eine Korrelation zwischen Absatz und Marktpreis ergeben, die im Zweifel geprüft werden sollte:

Andererseits ist die Temperatur ähnlich wie der Marktpreis ein Risikofaktor, der mit eigener Berechtigung überwacht werden sollte.

Wie bestimmt sich der Marktwert eines Vertriebskontraktes, wenn der Absatz zwar nicht direkt vom Marktpreis abhängt, aber doch mit diesem korreliert ist? Der Marktwert ergibt sich aus einem unsicheren Marktpreis und einem unsicheren Absatz, die beide miteinander korreliert sind. Der Marktwert M lässt sich somit als Zufallsgröße beschreiben. Wir suchen den Erwartungswert:

$E(M) = E((m - k) \cdot P )$
Der Kontraktpreis k ist konstant, m und P sind ihrerseits Zufallsgrößen. Es wird der Erwartungswert des Produktes von zwei Zufallsvariablen gebildet. Dieses Produkt berechnet sich als Produkt der Erwartungswerte plus die Kovarianz der Zufallsvariablen:

$E((m - k) \cdot P )= E(m-k) \cdot E(P) + Cov(m,P)$

Typischerweise wirken solche Korrelationen für den Lieferanten negativ: der Kunde zieht viel, wenn der Marktpreis hoch ist, und wenig, wenn er niedrig ist.

4. Klassische Call- und Put-Option

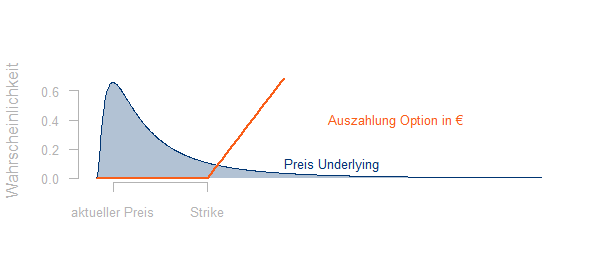
Im Falle klassischer Optionskontrakte ist der Zusammenhang zwischen Marktpreis und Liefermenge deterministisch: Eine Lieferung kommt zustande, sobald ein gewisser Preis erreicht, bzw. sobald ein gewisser Preis unterschritten ist. Eine Call-Option ist das Recht,

ein spezifiziertes Asset (Basiswert / Underlying)
zu einem spezifizierten Preis (Basispreis / Strike)
zu einem bestimmten Zeitpunkt (Fälligkeitstermin / Maturity)

zu kaufen. Eine Put-Option ist das entsprechende Verkaufsrecht. Betrachtet man als Underlying die klassischen Standardkontrakte Base und Peakkontrakte des Strom- und Gasterminmarktes, so kommt eine Lieferung genau dann zustande wenn der Strikepreis überschritten (Call) bzw. unterschritten (Put) ist.

Zum Fälligkeitstermin ist die Calloption wertlos, wenn der Strikepreis nicht erreicht wird. Wenn Preis des Underlyings den Strikepreis übertrifft, entspricht die Auszahlung einer Calloption (bzw. der Wert des eventuell physisch gelieferte Underlyings) der Differenz zwischen dem Preis des Underlyings und dem Strikepreis (rot):

Im Rahmen des traditionell verwendeten Black-Scholes-Modells wird zur Bewertung der Option angenommen, dass der Preis des Underlyings zum Fälligkeitstermin eine lognormalverteilte (blau) Zufallsvariable ist. Unter diesen Annahmen und einigen weiteren Annahmen kann dann der aktuelle Marktwert einer Standardoption explizit in Abhängigkeit von den folgenden Parametern bestimmt werden:

aktueller Marktpreis des Underlyings
Volatilität des Underlying-Preises
Laufzeit der Option
risikoloser Zinssatz

Der Wert ergibt sich im Wesentlichen, indem für jeden möglichen Marktwert des Underlyings die Wahrscheinlichkeit, mit der dieser Marktwert eintritt, mit der damit verbundenen Auszahlung multipliziert und abgezinst wird. Es ergibt sich eine explizite Darstellung des Marktwertes als Summe von zwei Integralen (siehe Wikipedia Black-Scholes-Modell).

Um das Black-Scholes-Modell anwenden zu können, sollten grundsätzlich die Voraussetzungen des Modells geprüft werden. Dazu gehört auch die Modellierung der Änderung des Underlyingpreises als lognormalverteilte Zufallsvariable. Siehe hierzu auch die Anmerkungen im Value-at-Risk-Kapitel.

5. Realoptionen

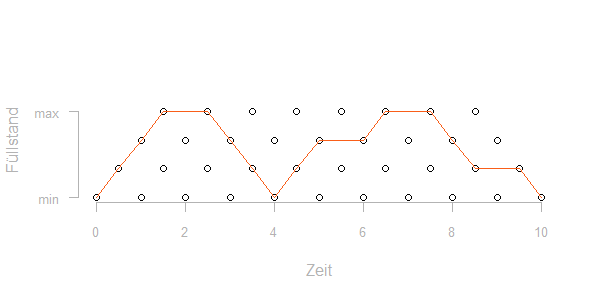
Kraftwerke und Speicher werden oftmals als Realoptionen bezeichnet. Ein Kraftwerk bietet die Möglichkeit, Gas, Kohle oder andere Brennstoffe in Strom zu wandeln, wenn die Marktpreise dies lukrativ erscheinen lassen. Ansonsten steht das Kraftwerk.

Ein Speicher bietet die Möglichkeit, Gas oder Strom zu einem Zeitpunkt einzuspeichern, an dem die Preise günstig erscheinen und zu einem späteren Zeitpunkt, an dem die Marktpreise höher sind wieder auszuspeisen.

Eine erste Näherung für den Marktwert solcher Realoptionen ergibt sich aus der optimalen Fahrweise bei derzeit gegebenen Terminpreisen (intrinsischer Wert). Dies resultiert für Speicher in einem Ein- und Ausspeisefahrplan, für Kraftwerke in einer Zeitreihe für den Brennstoffbedarf und einer Zeitreihe für die Stromerzeugung. Die Marktbewertung dieser Zeitreihen liefert eine untere Schranke für den Wert dieser Realoptionen. Die Ermittlung der genannten Zeitreihen erfolgt typischerweise über spezialisierte Systeme, siehe hierzu auch den Artikel zur Kraftwerkseinsatzoptimierung. Es wird ein optimales Ergebnis unter Einhaltung zahlreicher Nebenbedingungen gesucht. Diese sind z.B.

maximale An- und Abfahrrampen bzw.
maximale Ein- und Ausspeiseleistungen
Max- und Minleistung bzw.
maximales und minimales Speichervolumen

Das Optimierungsproblem wird durch stückweise lineare Gleichungen und Ungleichungen approximiert und mit dem Simplex-Algorithmus gelöst. Theoretische Erwägungen zeigen, dass das Maximum auf dem Rand des durch die Ungleichungen gebildeten Simplex liegen muss. Dies schränkt die Anzahl möglicher Fahrweisen ein und erlaubt die Suche eines Fahrplans mit maximalem Wert:

Die im Rahmen der Einsatzoptimierung ermittelten Strom- und Gaszeitreihen repräsentieren den aktuellen Wert des Assets Kraftwerks näherungsweise als Summe von:

Aufwand aus Terminkauf der Brennstoffe und der benötigten CO₂-Zertifikate
Erlös aus Terminverkauf der Stromzeitreihe

Eine solche Darstellung des Kraftwerks durch 2-3 Verträge (eine dritte für den Bedarf an CO₂-Zertifikaten), deren unterliegende Zeitreihen im Rahmen der Einsatzoptimierung ständig aktualisiert werden, ermöglicht die Absicherung der Marktrisiken des Kraftwerks mit Terminkontrakten. Für eine Absicherungsstrategie, die auch den Handel mit Optionen beinhaltet, muss die Marktrisikoposition des Kraftwerks genauer dargestellt werden. Entsprechendes gilt für Speicher.

Sensivitäten und die Deltaposition

Für die Steuerung von Marktrisiken ist eine Bewertung der Portfolien der erste Schritt. Der Wert des Portfolios ergibt sich als Summe der Assetbewertungen. Eigentlich von Interesse ist aber, wie der Marktwert von Assets und damit der Portfoliowert sich ändert, wenn sich die Marktpreise (oder andere Risikofaktoren) ändern.

1. Sensitivität gegenüber einem Risikofaktor

Was passiert mit dem Marktwert K eines Kontraktes, der von einem Risikofaktor abhängt, wenn sich dieser Risikofaktor r etwas ändert? Dafür wird der Marktwert K als Funktion von r dargestellt und die folgende Ableitung betrachtet:

$\frac{\partial }{\partial r} K$

In etwa ist der neue Marktpreis K dann

$K = K_0 + \delta r \cdot \frac{\partial }{\partial r} K$

wobei
K₀ der ursprüngliche Marktwerts
$\delta r$ die Änderung des Risikofaktors r

Den Wert dieser Ableitung bezeichnet man auch als Sensivität des Marktwertes auf Änderungen des Risikofaktors p.

2. Deltapositionen von Optionen

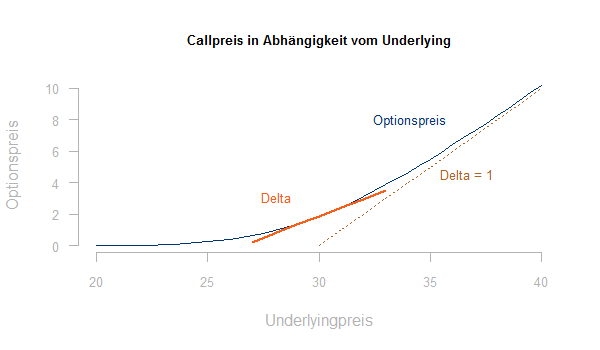
Eine spezielle Sensitivität ist die sogenannte Deltaposition. Sie bezeichnet für Derivate die Ableitung von dem Marktwert des Derivates K(p) nach dem Wert des Underlyings p.

$\Delta = \frac{\partial }{\partial p} K(p)$

Klassischerweise werden Deltapositionen für Optionen betrachtet. Für eine klassische Call- oder Putoption, deren Preis in € vom Marktpreis ihres Underlyings, z.B. einem Standard- Base- oder Peakkontrakt, in € abhängt, ergibt sich als Deltaposition eine Anzahl von Base- oder Peakkontrakten.

Handelt es sich um den Kauf einer klassische Call-Option auf einen Base- oder Peakkontrakt Strom oder Gas, so erhält man als Deltaposition eine Zahl zwischen 0 und 1. Eine „tief im Geld“ liegende Kaufoption (Call) hat ein Delta von fast +1, eine „tief im Geld“ liegende Verkaufsoption (Put) von fast -1.

Die Zahl repräsentiert die Anzahl Base- bzw. Peakkontrakte, die das Preisrisiko der Option bestmöglich approximieren. Um das Marktpreisrisiko aus dem Kauf einer Option abzusichern, sollte man somit immer eine Verkaufsposition in Höhe der jeweils aktuellen Deltaposition an Underlying-Kontrakten halten. Im Rahmen des Black-Scoles-Modells lässt sich auch das Delta einer Option explizit berechnen.

3. Deltapositionen von Realoptionen

Wie wir gesehen haben, beschreibt die Delta-Position einer klassischen Option die Position in Base- und Peakkontrakten, deren Wertänderungsverhalten dem der Option bestmöglich entspricht.

Dieselbe Aufgabenstellung interessiert bei der Absicherung der komplexen Realoptionen Kraftwerk und Speicher. Man möchte im Falle des Kraftwerks

einen Terminkauf eines Stromfahrplans
einen Terminverkauf eines Brennstofffahrplans und
einen Terminverkauf von CO2-Zertifikaten

so bestimmen, dass der Marktwert des Portfolios P aus diesen drei Kontrakten möglichst das gleiche Verhalten bei Änderung der Marktpreise hat wie der Wert K des Kraftwerks. Eine Änderung der Marktpreise bedeutet hier eine Änderung der HPFC und DFC-Preise, d.h. jedes einzelnen 1/4-h bzw. Tagespreises daraus. Konkret soll für jeden 1/4-h-Preis h_i der HPFC und jeden Tagespreis d_j der DFC, und die relevanten CO₂-Preise c_k gelten:

$\frac{\partial }{\partial h_i} P = \frac{\partial }{\partial h_i} K, \; \frac{\partial }{\partial d_j} P = \frac{\partial }{\partial d_j} K, \; \frac{\partial }{\partial c_k} P = \frac{\partial }{\partial c_k} K$

Leitet man den Marktwert von einem Terminkauf Strom nach dem i-ten HPFC-Preis ab, so erhält man genau den Lastwert an der Stelle i. Somit erhält man aus obigen Gleichungen als Deltaposition eines Kraftwerks einen Stromterminkauf mit den Lastwerten:

$(\frac{\partial }{\partial h_1} K, \frac{\partial }{\partial h_2} K, \cdots , \frac{\partial }{\partial h_{8760} }K)$

Die Terminverkäufe Gas und CO₂ definieren sich entsprechend aus der vollständigen Ableitung des Marktwertes nach den Gas- und CO₂-Preisen. Da sich der Marktwert des Kraftwerks jedoch nicht explizit berechnen lässt, liefert dies nur die Definition der Deltaposition. Die gesuchten Fahrpläne können nicht durch Ableitung ermittelt werden.

Praktisch erfolgt die Ermittlung der gesuchten Fahrpläne über die Softwaresysteme zur Einsatzoptimierung. In diesen wird zunächst mittels geeigneter Modelle eine ausreichende Anzahl HPFC / DFC / CO₂-Szenariopreise mit realistisch untereinander korrelierten Preisen generiert. Dann erfolgt die Ermittlung des optimalen Einsatzes und der daraus resultierenden Strom-, Gas-, CO₂ Fahrpläne im Prinzip (abgesehen von Maßnahmen zur Performance-Optimierung) für jedes der Szenarien einzeln über eine deterministische Optimierung. Zu jedem Preisszenario ergeben sich somit marktoptimale Fahrpläne, zugehörige Marktwerte und aus der Preisabweichung abgeleitete Differenzenquotienten. Aus diesen kann die Deltaposition ermittelt werden.

Portfoliowert-Analyse

Das Schöne an Delta-Positionen und Sensitivitäten ist, dass sie sich über das Portfolio addieren. Für den Marktwert K eines einzelnen Kontraktes, der als Funktion von Risikofaktoren r_i dargestellt werden kann, gilt (Taylor-Entwicklung):

$K = K_0 + \delta r_1 \cdot \frac{\partial }{\partial r_1} K + \delta r_2 \cdot \frac{\partial }{\partial r_2} K + \cdots$

wobei
K₀ der ursprüngliche Marktwert
$\delta r_i$ die Änderung des Risikofaktors $r_i$

Ebenso gilt für den Wert eines Portfolios P aus Kontrakten mit Marktwerten K_i:

$P = P_0 + \delta r_1 \cdot \frac{\partial }{\partial r_1} P + \delta r_2 \cdot \frac{\partial }{\partial r_2} P+ \cdots$

1. Offene Position

Die Ableitung des Portfoliowertes P eines Strom- oder Gasportfolios nach den HPFC- bzw. DFC-Preisen ergibt sich aus der Summe der Ableitungen der Einzelkontrakte:

$\frac{\partial }{\partial p_i} P = \sum_i \frac{\partial }{\partial p_i} K_i$

Im Fall von Terminlieferungen von Fahrplänen ergibt die vollständige Ableitung nach den HPFC-Preisen, wie wir gesehen haben, genau die Lieferzeitreihe (mit Vorzeichen). In Summe über das Portfolio ergibt sich die offene Position. Dabei können Deltapositionen aus Optionen und Realoptionen ebenso wie reguläre Fahrplanlieferungen behandelt und ebenfalls unter Beachtung des Vorzeichens addiert werden.

Die offene Position beschreibt die Sensitivität des Portfolios gegenüber jedem Einzelpreis der Forwardkurven.

2. Taylor-Entwicklung des Marktwertes

Wie wir bei der Bewertung einer einfachen Option gesehen haben, hängt der Wert eines Portfolios jedoch nicht nur von den aktuellen Forwardpreisen ab. Vielmehr hängt schon der Wert einer einfachen Calloption auf die Lieferung eines Standardkontraktes Base nach Black-Scholes-Modell ab von:

dem aktuellen Preis des Underlyings
der Volatilität des Underlyingpreises
der Laufzeit
dem Strike
und dem risikolosen Zins

Wir betrachten jedoch in diesem Abschnitt den funktionalen Zusammenhang zwischen dem Portfoliowert und den aktuellen Forwardpreisen r_i. Das heißt der Portfoliowert P ist zunächst eine Funktion

$P: \mathbb{R}^n \to \mathbb{R}$

die aus Werten der Risikofaktoren (Forwardpreise) r₁, … r_n den Portfoliowert ermittelt. Alle anderen Parameter wie z.B. Volatilitäten werden dabei als fest betrachtet.

Der Portfoliowert als Funktion der Werte von eingehenden Risikofaktoren kann dann in einer Taylor-Entwicklung dargestellt werden. Das Taylorpolynom bis zur 2ten Ordnung beschreibt die Änderung von P in Abhängigkeit der Änderung der relevanten Risikofaktoren r_i im selben Zeitraum näherungsweise als:

$\delta P = \sum_i {\delta r_i \cdot \frac{\partial }{\partial r_i } P} + \frac{1}{2} \sum_{i,j} {\delta r_i \cdot \frac{\partial^2 }{\partial r_i \partial r_j}P \cdot \delta r_j} + \cdots$

Mit einer solchen Darstellung lässt sich die Wertänderung erklären durch

Bestandteile, die aus der Strompreisänderung kommen (Strompreisänderung mal Deltaposition Strom)
Bestandteile, die aus der Gaspreisänderung kommen (Gaspreisänderung mal Deltaposition Gas)
Bestandteile, die aus der CO₂ -Preisänderung kommen (CO₂ – Preisänderung mal Deltaposition CO₂ )

Die Taylorentwicklung kann nicht nur für das Portfolio als Ganzes, sondern auch für jedes enthaltene Asset in dieser Form durchgeführt werden. Die einzelnen Summanden der Taylorentwicklung des Portfoliowertes ergeben sich als Summe der entsprechenden Summanden aus der Taylorentwicklung der enthaltenen Einzelkontrakte. So werden sie in der Regel auch praktisch ermittelt.

Eine solche Rückführung von Portfoliowertänderungen von einem Tag auf den anderen auf Änderungen der Risikofaktoren im selben Zeitraum kann verwendet werden, um das Tagesergebnis eines Portfolios, d.h. die Wertveränderung von einem Berichtszeitpunkt zum nächsten, zu erklären.

3. Greeks

Auch Änderungen der Volatilitäten und die Verkürzung der Laufzeit von Optionen können zu einer Marktwertänderung des Portfolios führen. Auch nach den Volatilitäten der Risikofaktoren und nach der Zeit kann abgeleitet werden. Weiterhin zeigt die Weiterentwicklung der Taylorentwicklung zu Thermen zweiter Ordnung, dass auch höhere Ableitungen relevant sein können. Alle diese möglicherweise relevanten Ableitungen nennt man Greeks. Für Terminkäufe und -verkäufe ohne Optionsbestandteile sind alle Greeks außer Delta Null.

Delta ist die Ableitung von dem Marktwert eines Optionskontraktes K nach dem Marktpreis des Underlyings p:

$\Delta = \frac{\partial }{\partial p } K$

Im Rahmen der Risikobewertung eines Portfolios bezeichnet man als Delta den Vektor der partiellen Ableitungen des Portfoliowertes nach den Risikofaktoren:

$\Delta_i = \frac{\partial }{\partial r_i } P$

Gamma ist die zweite Ableitung von dem Marktwert eines Optionskontraktes K nach dem Marktpreis des Underlyings p:

$\Gamma = \frac{\partial^2 }{\partial p^2 } K$

Im Rahmen der Risikobewertung eines Portfolios bezeichnet man als Gamma die Matrix aller zweiten Ableitungen des Portfoliowertes nach den Risikofaktoren:

$\Gamma_{ij}= \frac{\partial^2 }{\partial r_i \partial r_j} P$

Vega ist die Ableitung von dem Marktwert eines Optionskontraktes K nach der Volatilität v des Underlyingpreises:

$V = \frac{\partial }{\partial v } K$

Theta ist die Ableitung von dem Marktwert eines Optionskontraktes K nach der Laufzeit t:

$\Theta = \frac{\partial }{\partial t } K$

Auch diese Kennzahlen können wie Delta für jeden Einzelkontrakt bestimmt und dann über das Portfolio aggregiert werden.

Der Value-at-Risk

Es können somit auf Portfolioebene eine Vielzahl von Risikokennzahlen bestimmt werden, die das Verhalten des Portfoliowertes bei Veränderung einzelner Risikofaktoren detailliert beschreiben. Diese Risikokennzahlen sind für die operative Steuerung der Marktrisiken zweckmäßig. Allerdings geben sie keine direkte Auskunft darüber, ob das Gesamtrisiko eines Portfolios noch vertretbar oder schon zu hoch ist. Somit sind diese durch Ableitungen definierten Risikokennzahlen nicht wirklich managementtauglich.

1. Definition des Value-at-Risk

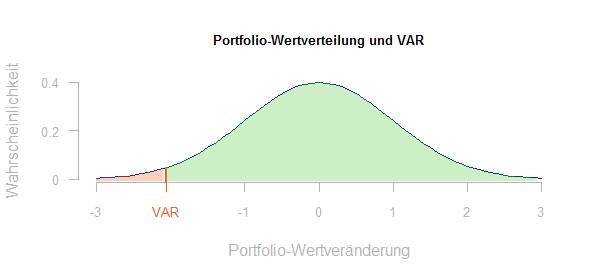
Auf Managementebene wünscht man sich eine einzige Kennzahl für das Portfolio, die in etwa Auskunft auf die folgende Frage gibt:

Wieviel werde ich mit sehr hoher Wahrscheinlichkeit (Konfidenzniveau) in den nächsten x Tagen (Haltedauer) höchstens verlieren, wenn ich in dieser Zeit meine derzeitigen Risikopositionen nicht verändere?

Dabei wird davon ausgegangen, dass die Portfoliowertveränderung während der Haltedauer einer stochastischen Verteilung unterliegt, die aus historischen Daten ermittelt werden kann. Auf diese Weise kann dann eine maximale negative Wertveränderung bestimmt werden, die mit der in dem Konfidenzniveau festgelegten Wahrscheinlichkeit nicht überschritten wird.

Üblicherweise wird mit Konfidenzniveaus von 95% oder 99% und mit Haltedauern von 1 Tag, 10 Tagen oder einem Monat gerechnet. Die Haltedauer sollte die Marktliquidität und tatsächliche Reaktionszeiten bei der Portfoliobewirtschaftung wiederspiegeln.

2. Historisches VAR-Modell

Weit verbreitet in der Energiewirtschaft ist der historische VAR. Dabei werden aus historischen Wertänderungen aller Risikofaktoren mögliche künftige Werte dieser Risikofaktoren generiert. Für eine Folge historischer Werte w₁, … , wn für einen Risikofaktor r erhält man eine Folge von Änderungen dieses Risikofaktors

$\Delta w_1, \dots \Delta w_{n-1}$

Unterstellt man eine Lognormalverteilung für den Wert des Risikofaktors am Ende der Haltedauer, so sollte man hier relative Änderungen betrachten. Für Energiepreise ist allerdings die Annahme einer Lognormalverteilung weniger zwingend als beispielsweise für dividendenlose Aktienpreise. Spotpreise zeigen negative Werte und sind bereits deshalb nicht lognormalverteilt. Auch Terminpreise lassen sich nicht konsistent lognormalverteilt modellieren: Wenn Monatsterminpreise lognormalverteilt sind, so sind Jahresterminpreise eine Linearkombination dieser Preise. Eine Linearkombination lognormalverteilter Zufallsvariablen ist nicht lognormalverteilt.

Durch Anwendung der historischen Änderungen jedes Risikofaktors auf seinem aktuellen Wert ermittelt sich eine Folge möglicher künftiger Werte des Risikofaktors. Bei Betrachtung aller Risikofaktoren ergeben sich n-1 zueinander passende mögliche künftige Szenarien, die die Korrelationen zwischen den Risikofaktoren implizit berücksichtigen.

Mit diesen Preisszenarien kann das Portfolio bewertet werden. Man erhält eine Folge von n-1 möglichen Portfoliowerten. In Abhängigkeit von dem Konfidenzniveau k (z.B. k = 95%) werden der (1 – k)-te Teil der schlechtesten Werte nicht berücksichtigt. Der schlechteste noch verbleibende Wert – bzw. die zugehörige Wertänderung – ist der Value-at-Risk.

Als historische Risikofaktoren können die Preisforwardkurven (HPFC, DFC) der Vergangenheit verwendet werden. Es können aber auch nur die in die Terminkurve eingehenden Base, und Peak- Preise als Risikofaktoren betrachtet werden. Die Generierung der Forwardkurve ist dann bereits Teil der Bewertung.

Der einfachste Fall ist die Risikobewertung eines Portfolios ohne optionale Bestandteile. Verwendet man als historische Risikofaktoren die Preisforwardkurven, so hängt der Wert des Portfolios linear von der zur Bewertung verwendeten Preisforwardkurve ab. Die Berechnung des historischen VAR entspricht dann der Bewertung des Portfolios mit n historischen Preisforwardkurven und der Ausgabe des durch das Konfidenzniveau vorgegebenen Quantils von Wertänderungen.

2. Varianz-Covarianz-Methode

Bei der Varianz-Covarianz-Methode wird eine Reduzierung in Datenhaltung und Rechenaufwand erreicht, indem man auf Verteilungsannahmen der eingehenden Risikofaktoren und deren Korrelation zurückgreift. Dem liegt wieder die bereits oben angeführte Taylor-Entwicklung zugrunde, die die Portfoliowertänderung auf Änderungen der Terminpreise zurückführt:

$\delta P = \sum_i {\delta r_i \cdot \Delta_i^P} + \frac{1}{2} \sum_{i,j} {\delta r_i \cdot \Gamma_{i,j}^P \cdot \delta r_j} + \cdots$

Betrachtet man die Portfoliowertänderung als Zufallsvariable, so ergibt sie sich laut dieser Gleichung rechnerisch aus diversen Konstanten (den Deltas und Gammas) und den Wertänderungen der Terminpreise r_i, die ihrerseits Zufallsvariablen sind. Ist die Varianz und Covarianz der Zufallsvariablen r_i bekannt, so lässt sich die Varianz der Zufallsvariable Portfoliowertänderung hieraus berechnen.

Berücksichtigt man zunächst nur die Terme erster Ordnung, so ergibt sich die Portfoliowertänderung als eine Linearkombination aus den Wertänderungen der Zufallsvariablen r_i:

$\delta P = \sum_i {\delta r_i \cdot \Delta_i^P}$

Gemäß der Definition der Varianz ergibt sich die Varianz einer solchen Linearkombination von Zufallsvariblen als:

$V(\delta P) = \sum_{i,j} \Delta_i^P \cdot Cov(\delta r_i, \delta r_j) \cdot \Delta_j^P$

Für diese Bestimmung der Varianz sind keine Verteilungsannahmen für die Risikofaktoren notwendig. Um aus einer Varianz der Portfoliowertänderungen das für den Value-at-Risk erforderliche Quantil ermitteln zu können, ist allerdings die Annahme erforderlich, dass die Portfoliowertänderung normalverteilt ist. Für eine normalverteilte Zufallsvariable ergeben sich alle Quantile aus Varianz und Mittelwert (0). Dieses Verfahren zur Ermittlung des Value-at-Risk heißt Delta-Normal-Methode.

Um ein solches Verfahren praktisch anzuwenden, muss die Korrelationsmatrix der Risikofaktoren ermittelbar sein. Somit werden bei einem solchen Verfahren typischerweise die Preise gehandelter Standardprodukte als Risikofaktoren betrachtet. Die Deltaposition eines Portfolios in einem solchen Standardprodukt entspricht dem optimalen Hedge des Portfolios in diesem Standardprodukt, d.h. das Portfolio wird durch eine Position in Standardprodukten approximiert.

Mit deutlich mehr Aufwand können auch die Gamma-Anteile eines Portfolios berücksichtigt werden. Das entsprechende Verfahren heißt Delta-Gamma-Methode.

3. Grenzen des VAR

Neben den hier erwähnten Verfahren gibt es viele weitere Varianten zur VAR-Berechnung. Üblich sind z.B. Monte-Carlo-Simulationen, in denen für Risikofaktoren Modelle für das stochastische Verhalten ausgewählt und kalibriert werden und die Portfoliobewertung dann auf einer Vielzahl generierter Szenarien basiert. Einfache Verfahren werden oft mit Sicherheitsfaktoren und diversen Korrekturen des Ergebnisses oder der Eingangsdaten modifiziert. Auch raffinierte und rechenaufwändige Verfahren beinhalten jedoch regelmäßig – teilweise unbewusst und undeklariert – Normalverteilungsannahmen und haben oftmals Schwächen in der Wiedergabe der Korrelationen.

Der Value at Risk ist ein nicht subadditives Risikomaß. Die Summe der VaR-Werte von Teilportfolien kann kleiner sein, als der VaR-Wert des Gesamtportfolios. Dieser Effekt kommt aus der Quantilbildung. In Teilportfolien können hohe negative Ergebnisse aussortiert werden, weil sie nicht im betrachteten Quantil liegen, die bei Betrachtung des Gesamtportfolios wieder eingehen.

Grundsätzlich setzt eine VAR-Steuerung liquide Märkte voraus. In illiquiden Märkten sind Volatilitäten von Risikofaktoren, die das Herz aller VAR-Modelle darstellen, nicht messbar. Man fährt in diesem Falle mit Positionslimits besser.

Weiterhin schaut der VAR wie alle statistischen Risikomaße in die Vergangenheit, um die Zukunft zu bestimmen. Gibt es einen Grund, Preisschocks in naher Zukunft zu erwarteten, die nicht den Vergangenheitsdaten entsprechen, sichert man sich ebenfalls besser mit Positionslimits. Auch Korrelationen entsprechen in der Zukunft und im Krisenfall nicht immer den Korrelationen, die man in der Vergangenheit und in guten Zeiten gemessen hat.

Portfoliostrukturen

1. Das Portfolio als Bewertungsbasis

2. Anforderungen an die Portfoliodarstellung

Marktbewertung von Assets

1. Terminkontrakte

2. Vertriebskontrakte mit marktpreisunabhängiger Absatzmenge

3. Marktpreiskorrelierte Vertriebskontrakte

4. Klassische Call- und Put-Option

5. Realoptionen

Sensivitäten und die Deltaposition

1. Sensitivität gegenüber einem Risikofaktor

2. Deltapositionen von Optionen

3. Deltapositionen von Realoptionen

Portfoliowert-Analyse

1. Offene Position

2. Taylor-Entwicklung des Marktwertes

3. Greeks

Der Value-at-Risk

1. Definition des Value-at-Risk

2. Historisches VAR-Modell

2. Varianz-Covarianz-Methode

3. Grenzen des VAR

Gefällt mir:

Kommentar verfassenAntwort abbrechen