Lastprognose- und Forecastverfahren

In der Energiewirtschaft werden fast alle entscheidenden Daten durch Zeitreihen beschrieben. Die Fortschreibung dieser Zeitreihen und die Qualität der Prognosen und Forecastverfahren bestimmt entscheidend das finanzielle Ergebnis.

Prognosen und Forecastverfahren werden routinemäßig für die kurzfristige und langfristige Prognose von Lastgängen benötigt. Weiterhin werden oftmals auch Spot-, Regel- und Ausgleichsenergiepreise mit ähnlichen Verfahren in die Zukunft geschrieben. Die folgende kleine Einführung in das Thema Zeitreihenanalyse und Forecasts beinhaltet:

• Analyse und Visualisierung der historischen Daten
• Einfache Prognoseverfahren
• Temperaturregression der TU-München
• Lineare Regression, Autoregression, ARIMA
• Messung der Prognosegüte
• Ausblick und weiterführende Links

Analyse und Visualisierung der historischen Daten

Der erste Schritt bei der Erstellung einer Prognose sollte stets in der Analyse und Visualisierung der historischen Daten bestehen. Die Visualisierung ermöglicht, Datenfehler und Ausreißer zu erkennen und Muster in den Daten zu finden.

1. Visualisierung von Zeitreihen

Für Zeitreihen ist die erste naheliegende Darstellung der Zeitreihenplot. Eine solche Visualisierung zeigt:

• Trends
• Ausreißer
• Einflussfaktoren (temperaturabhängig oder nicht)
• Saisonalität (Jahres- und Wochenstrukturen)

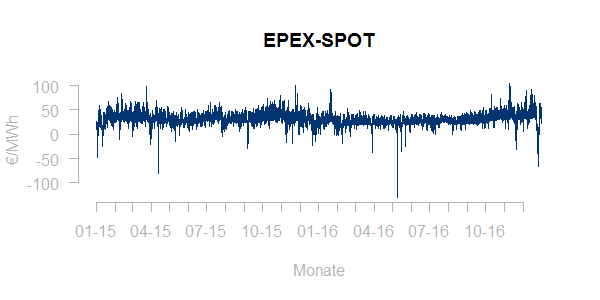
Hier z.B. eine Historie der Spotpreise über die Jahre 2015-2016:

Die Spotpreise zeigen offensichtlich Ausreißer aber keinen deutlichen Trend und erstaunlicherweise keine Abhängigkeit von der Jahreszeit. Insgesamt bleibt es eine Ermessensfrage, inwieweit extreme Preise als Ausreißer oder als Teil der normalen Volatilität der Preise gewertet werden sollten. Es ist somit wichtig, der Ursache von extremen Ereignissen genauer nachzugehen, um zu entscheiden, ob diese bereinigt werden sollen und unter welchen Umständen solche Ereignisse in Zukunft zu erwarten sein könnten und somit in den Forecast integriert werden müssen.

 

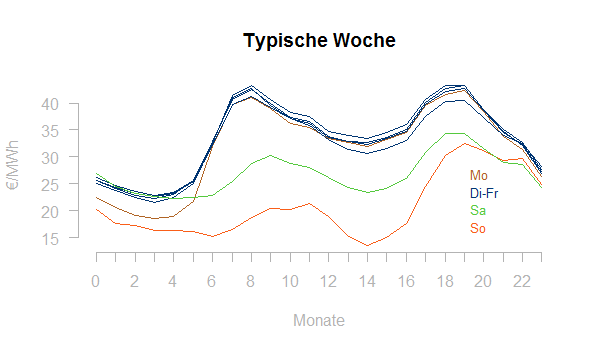
Zeitreihen in der Energiewirtschaft haben häufig sogenannte Saisonalitäten, d.h. sie zeigen im Jahresverlauf wiederkehrende typische Strukturen. Die Darstellung der typischen Woche zeigt den typischen (d.h. durchschnittlichen) Montag, Dienstag, … , Samstag, Sonntag. Hier wieder für die EPEX-Spotpreise:

Man erkennt:

• den im Durchschnitt deutlich anderen Preisverlauf am Wochenende (Samstag und Sonntag)
• den tiefen Einstieg am Montag morgen
• den leichten Preisabfall am Freitagnachmittag
• sowie die sehr vergleichbare Last Dienstag-Donnerstag

Die typische Woche gibt einen ersten Einblick, ob eine Last- oder Preiszeitreihe überhaupt Tages- und Wochensaisonalität besitzt und wie stark diese ausgeprägt ist.

 

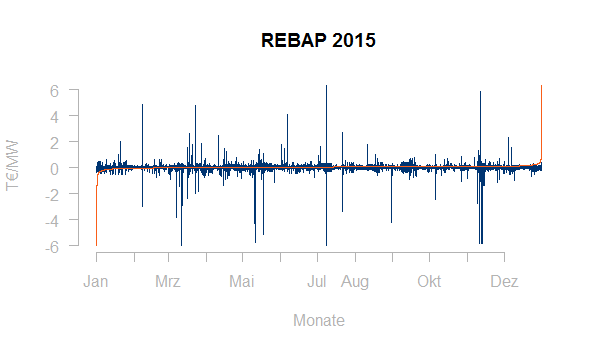
Üblich ist in der Energiewirtschaft weiterhin die Darstellung von Zeitreihen als geordnete Ganglinie. Hier werden alle Last- oder Preiswerte einfach der Größe nach geordnet angezeigt. Oftmals wird eine solche Ganglinie zusammen mit dem Zeitreihenplot in einer Graphik gezeigt. Hier die Ausgleichsenergiepreise im Jahr 2015 zusammen mit einer geordneten Ganglinie:

 

Geordnete Ganglinien lassen sich leicht optisch beurteilen, datenreduziert darstellen (z.B. mit Fourier-Analyse) und sind somit auch für ein erstes Clustering von Lastgängen geeignet.

2. Beurteilung der Verteilung von historischen Daten

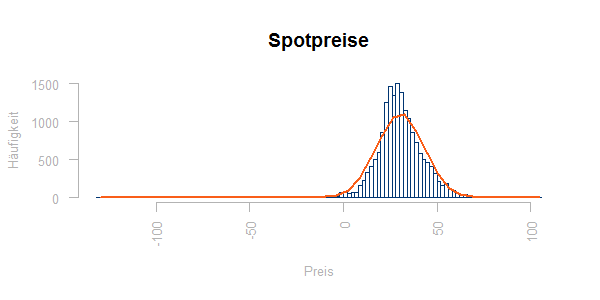
Die Verteilung von Last- und Preiswerten zeigt ein Häufigkeitsdiagramm. Hier die Verteilung der Spotpreise gegen eine Normalverteilung mit gleichem Mittelwert und gleicher Streuung:

Man sieht Abweichungen von der Normalverteilung um den Mittelwert herum, die Ausreißer lassen sich in dieser Darstellung kaum beurteilen.

 

Es ist somit hilfreich, die Häufigkeitsverteilung auch tabellarisch auszuwerten, z.B. über die Quantilwerte:

 

0%	10%	20%	30%	40%	50%	60%	70%	80%	90%	100%
-130,090	16,439	21,948	24,700	27,090	29,610	32,024	35,060	39,452	45,960	104,960

 

3. Abhängigkeiten und Korrelationen

Neben der Verteilung der Daten interessiert natürlich die Abhängigkeit der Preise und Lasten von Wetterdaten, kalendarischen Informationen oder anderen Einflussfaktoren. Viele Lastzeitreihen zeigen eine deutliche Abhängigkeit zur Temperatur. Zur Darstellung von Abhängigkeiten dient das Punktediagramm.

 

Bei den Ausgleichsenergiepreisen erwartet man zunächst eine Abhängigkeit vom Regelzonensaldo:

Tatsächlich hat der Regelzonensaldo nicht den erwünschten Erklärungsgehalt. Extreme positive und negative Ausgleichsenergiepreise zeigen sich vorrangig bei einem Regelzonensaldo nahe Null.

 

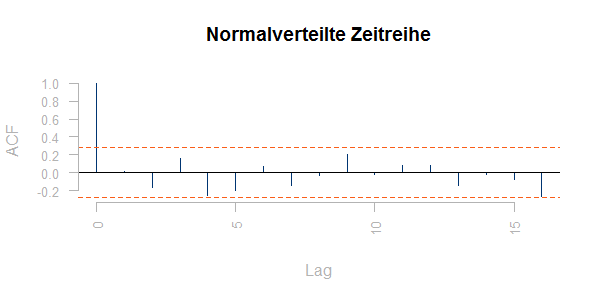
Interessant ist auch die Autokorrelation einer Zeitreihe; diese gibt an, in wieweit vergangene Werte die künftigen Werte bestimmen. Man kann die Autokorrelationskoeffizienten einer Zeitreihe plotten. Dabei wird jeweils die Korrelation zwischen dem Wert in der Position i und dem Wert in der Position i + n für alle „Lags“ n geplottet. Für eine Zeitreihe aus unabhängig, standardnormalverteilt streuenden Werten sieht ein solcher Plot so aus:

 

Die empirischen Korrelationen zwischen den Werten sind klein, aber nicht null. 95% der Balken sollten innerhalb  von

liegen (roter Korridor), dabei ist T die Länge der Zeitreihe.

 

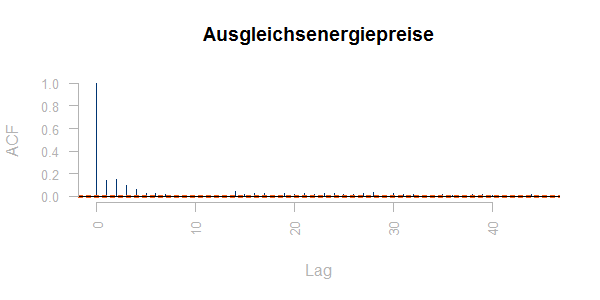
Im Gegensatz zu diesem Referenzbeispiel sind die Ausgleichsenergiepreise deutlich autokorreliert:

4. Ausreißer und Ausnahmewerte

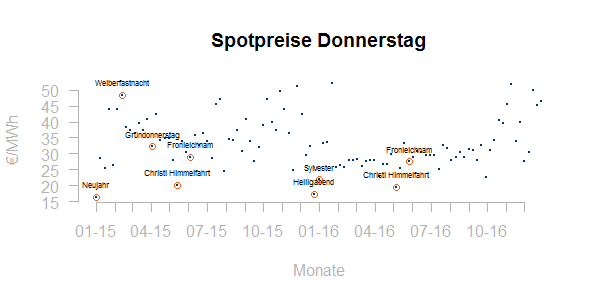
Für die Beurteilung von Ausreißern ist es zweckmäßig, Datenpunkte zu beschriften. Zum Beispiel ist es für eine HPFC/DFC-Entwicklung relevant, welche Tage eigentlich als Feiertage gewertet werden sollten. Nicht alle Feiertage sind bundesweit und auch bundesweite Feiertage spielen unter Umständen in einem europaweit gekoppelten Strommarkt keine Rolle. Hier das Tages-Spotpreisniveau für die Donnerstage 2015-2016 im Zeitverlauf:

Viele Feiertage befinden sich in guter Gesellschaft mit ihren Nachbarn. Andere – wie die Weiberfastnacht – scheinen wenn überhaupt nach oben auszureißen.

Einfache Prognoseverfahren

Das zunächst einmal naheliegendste Forecastverfahren ist immer die Fortschreibung von Vergangenheitswerten. Hierbei können je nach Bedarf Trends und Saisonalitäten berücksichtigt werden.

1. Einfache Fortschreibung

Eine einfache Fortschreibung kommt für eine kurzfristige Prognose in Frage, wenn die Daten keine Saisonalität besitzen. Die Prognose ist hier immer der jeweils letztgemessene Wert.

 

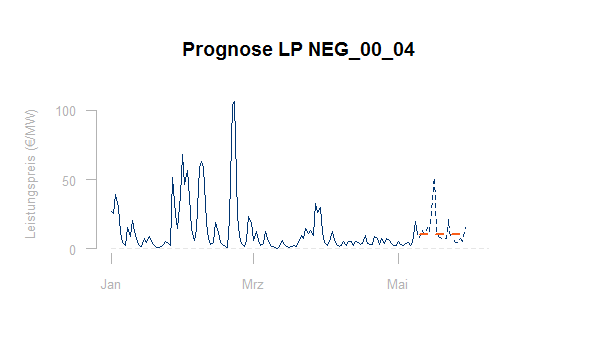
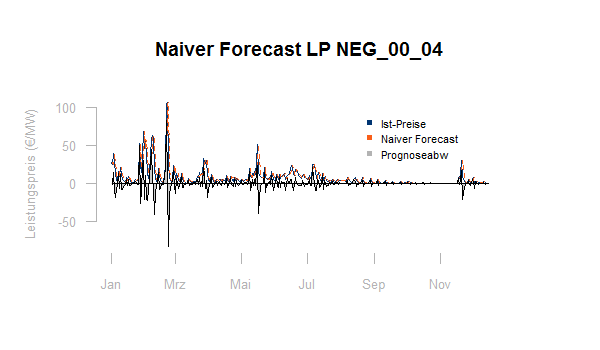
Die Graphik zeigt eine einfache Fortschreibung für den Minutenreservepreis des Produktes NEG_00_04 (siehe den Artikel zum Regelmarkt):

 

Natürlich kann auch ein geeigneter Mittelwert aus dem Zeitfenster der letzten x Werte in die Zukunft geschrieben werden. Da man im Regelmarkt den entstehenden Preis nie übertreffen darf, kann es hier auch sinnvoll sein, als Prognose ein geeignetes Quantil der letzten Preise zu verwenden. Das Zeitfenster über das gemittelt oder ein Quantil gebildet wird, kann aus der Historie ergebnisoptimal gewählt werden.

 

Eine weitere Möglichkeit ist, die gesamte Historie zu berücksichtigen, aber kürzliche Werte höher zu gewichten als weiter in der Vergangenheit liegende. Dies bezeichnet man als Exponentielle Glättung. Für einen Parameter α ergibt sich der Forecast von y zum Zeitpunkt t+1 dann als:

Dabei liegt α zwischen 0 und 1, je höher α desto mehr Gewicht wird den jüngsten Werten gegeben.

2. Typtagsprognosen

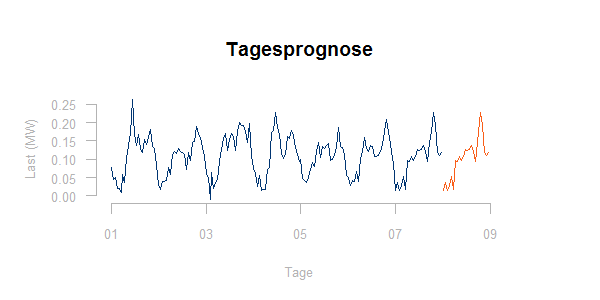
Energiewirtschaftliche Daten haben typischerweise eine Tages-, Wochen- und Jahressaisonalität. Entsprechend sind sogenannte Typtagsprognosen in vielen Fällen der erste Ansatz. Weite Verbreitung haben sie bei der Tagesprognose von Lastgängen.

 

Die Typtagsprognose prognostiziert im einfachsten Fall den Lastverlauf eines Montags- entsprechend dem vergangenen Montag, den Lastverlauf am Dienstag entsprechend dem vergangenen Dienstag usw.

 

Oftmals kommen noch die namensgebenden Typtage zur Anwendung, d.h. die Tage werden aufgeteilt nach:

• Montag
• Dienstag – Donnerstag
• Freitag
• Samstag
• Sonn- und Feiertag

Wieweit eine solche Aufteilung berechtigt ist, muss eine Analyse vergangener Daten zeigen. Die Prognose eines Tages entspricht jedenfalls dann der Last des nächsten vergangenen Tages mit gleichem Typtag:

3. Fortschreibung von Trends

Hat die Zeitreihe einen eindeutigen Trend, so kann dieser Trend fortgeschrieben oder – wenn die Fortsetzung nicht wahrscheinlich ist – auch bereinigt werden. Bei Lastdaten ist es sinnvoll, Ursachen von Lasttrends und die weitere Aussicht mit dem Kunden abzuklären. Bei Preisdaten wird der Trend oftmals als zufällig, d.h. als Teil der Volatilität, interpretiert.

Temperaturregression der TU-München

Schwieriger wird die Lastprognose, wenn die Last offensichtlich temperaturabhängig ist. Beim Gasverbrauch ist dies der typische Fall. Deshalb wurden von der gleichnamigen Universität die TU-München Profile entwickelt, die nach GasNZV für die Abwicklung von SLP-Gaskunden empfohlen werden. Diese Profile modellieren die Temperaturabhängigkeit der Tageslast in Abhängigkeit von einer gemittelten Temperatur, die auch Vortageswerte enthält mittels einer sogenannten Sigmoidfunktion. Dieses Modell ist auch für die Prognose temperaturabhängiger RLM-Kunden Gas oder für die Modellierung der Temperaturabhängigkeit des Fernwärmeabsatzes interessant.

1. Bestimmung der anwendbaren Temperatur

Temperaturabhängigen Lasten muss vor Erstellung einer Prognose eine sinnvolle Wetterstation zugeordnet werden. Für die Modellparametrierung benötigt man eine ausreichende Historie (i.a. 2 Jahre) von Wetterdaten.

Die TU-München Profile verwenden als anwendbare Temperatur den folgenden Mittelwert:

hierbei ist T_t die Tagestemperaturprognose für den Liefertag, T_t-1 bisT_t-3 jeweils die Tagestemperaturen der Vortage.

 

Die Berücksichtigung der Vortagestemperaturen stellt die Berücksichtigung der Wärmespeicherfähigkeit von Gebäuden sicher. Die Gewichtungsfaktoren vor den Einzeltemperaturen sind Modellparameter, die für eine Individualprognose prinzipiell auch individuell optimal auf Basis von Vergangenheitswerten kalibriert werden können.

2. Das Sigmoid-Modell

Im Rahmen der TU-München-Profile ergibt sich die Tageslast L multiplikativ als:

wobei der Faktor l₀ temperaturunabhängig ist und entweder konstant ist oder nur vom Wochentag abhängt.

 

Die Temperaturabhängigkeit der Last wird durch die Signoidfunktion h beschrieben, dabei ist:

Die unterschiedlichen TU-München-Profile unterscheiden sich durch unterschiedliche Wahl der Parameter und A, B, C und D und Wochentagsfaktoren zur Bestimmung von l₀, jeweils mit der Basistemperatur:

Für die Fortschreibung von SLP-Kunden werden insgesamt 62 konkrete Profile, d.h. konkrete Setzungen der Parameter A, B, C und D und gegebenenfalls von Wochentagsfaktoren vorgegeben und Branchen zugeordnet, aus denen der Ausspeisenetzbetreiber für sein Netzgebiet wählen kann. Hiermit kann ein breites Spektrum von Temperaturabhängigkeit abgebildet werden. Hier die Werte der h-Funktion in Abhängigkeit von der Temperatur für einige Branchenprofile mit der Ausprägung 04 (siehe Leitfaden Abwicklung von Standardlastprofilen Gas):

 

Das durch die Signoidfunktion abgebildete grundsätzliche Prinzip ist, dass die Last auch für beliebig kalte Tage immer höchstens den maximal möglichen Wert erreichen kann, der durch die installierte Heizleistung vorgegeben ist:

Die Basistemperatur wird mit 40 °C so hoch gesetzt, dass sie in unseren Breiten nicht erreicht werden kann. Die Sigmoidfunktion zeigt für warme Temperaturen den Grenzwert:

Die Parameter B und C kontrollieren die genaue Form der S-Kurve bei mittleren Temperaturen.

3. Parametrierung des Sigmoid-Modells

Sowohl der Ausspeisenetzbetreiber, der aus den pro Branche bis zu 5 Standardprofilen der TU-München das richtige auswählen muss, als auch der Energievertrieb, der einen temperaturabhängigen Großkunden oder den Fernwärmeabsatz mit freigewählten Methoden prognostizieren kann, stehen vor der Aufgabe die Parameter des Modells richtig zu wählen. Dies geschieht im Wesentlichen in beiden Fällen auf gleiche Weise.

 

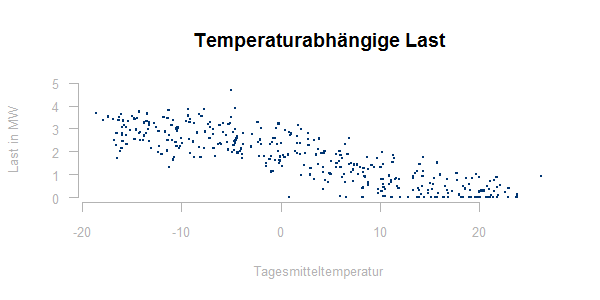
Wie immer, wenn die Abhängigkeit der zu prognostizierenden Größe von anderen Parametern untersucht werden soll, visualisieren wir den Zusammenhang zunächst über ein Punktediagramm. Für einen temperaturabhängigen Lastgang könnte ein solches Punktediagramm wie folgt aussehen:

In diese Punktwolke muss nun eine Kurve eingepasst werden, die die Temperaturabhängigkeit der Last bestmöglich beschreibt. Hierzu verwenden wir die Methode der kleinsten Quadrate, d.h. die Parameter der Sigmoid-Funktion werden so gewählt, dass für die gemessenen Lastwerte L bei der Temperatur t die folgende Summe minimiert wird:

Ein Least-Square-Fit ist in statistischer Software (z.B. R) standardmäßig implementiert. Zweckmäßiger setzt man die Parameter eines optisch passenden TU-München Standardprofils als Startwerte (st), um Konvergenz und sinnvolle Rechenzeit zu erreichen. Mit den Werten (werte) der Punktwolke mit den Koordinaten Temperatur (temp) und Last (y) erhält man dann die genau optimalen Parameter in R über die Zeilen:

h ← function(a, b, c, d, t, t0){
(a/(1+ (b/(t-t0))^c)) + d
}
nls(y ~ h(a, b, c, d, temp, 40), start =st, data = werte)

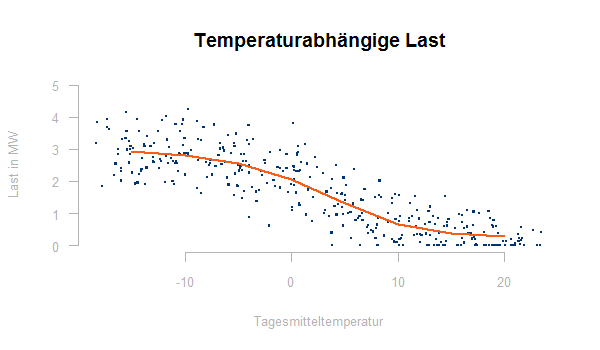
Das Ergebnis sieht so aus:

Es ist sinnvoll den Rest y – konst * h(t) gegen die Temperatur zu plotten, dieser sollte keine Temperaturabhängigkeit mehr enthalten, andernfalls ist der Fit durch eine Sigmoidfunktion nicht adäquat.

 

Weiterhin sollte der Rest als Zeitreihe geplottet und auf weitere Muster und Strukturen geprüft werden.

Lineare Regression, Autoregression, ARIMA

Lineare Regression ist sicherlich eines der Arbeitspferde, wenn es um die Erstellung von Lastprognosen geht. Auch bei der Prognose von Preisen kommen lineare Regression und die verwandten autoregressiven Modelle oft zum Einsatz.

1. Lineare Regression

Bei einer linearen Regression wird eine abhängige Variable y über k unabhängige x-Variablen mit zugehörigen Konstanten α prognostiziert. Die zentrale Gleichung lautet dabei:

dabei sind e_i unkorrelierte Werte einer normalverteilten Zufallsvariable e mit Erwartungswert 0 und konstanter Varianz.

 

Um ein lineares Regressionsmodell zur Prognose von y aufzusetzen, müssen zunächst mögliche Kandidaten für die x-Variablen gefunden werden. Hierzu benötigt man Daten, die im Gegensatz zu y zum Prognosezeitpunkt bekannt sind und eine hohe Korrelation zu y besitzen.

 

Sind die x-Variablen gefunden, so bestimmt man die α-Konstanten wiederum durch die Methode der kleinsten Quadrate, minimiert wird:

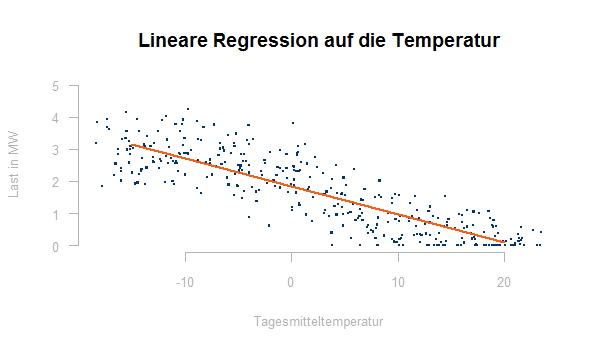
Auch diese Kalibrierung bietet mathematische Software üblicherweise an, in R erhält man eine lineare Regression auf die Temperatur für die oben gezeigte temperaturabhängige Last mit:

fit ← lm(y ~ temp, data=werte)
summary(fit)

Das Ergebnis sieht so aus (nicht ganz so schön, wie die Sigmoid-Funktion der TU-München):

Nach der Kalibrierung sollten die Restterme e_i gegen die Prognosevariablen x geplottet werden. Dieser Plot sollte keine Muster mehr erkennen lassen, sonst ist dies ein Hinweis auf nichtlineare Zusammenhänge zwischen y und den x-Variablen.

 

Eine Regression ist auch auf diskrete x-Variablen möglich, beispielsweise kann als unabhängige Variable ein Feiertagsindikator  verwendet werden, der den Wert 1 am Feiertag annimmt und 0 sonst.

 

Problematisch ist eine Regression auf x-Variablen, die untereinander stark korreliert sind. Die Korrelationsgleichung ist dann nicht eindeutig lösbar oder es ergeben sich unplausible Koeffizienten (negative Abhängigkeit, wo positive Abhängigkeit zu erwarten wäre).

2. AR- und ARIMA-Modelle

Eine kleine Abwandlung des vorher beschriebenen Modells ist die Prognose einer Variable y mit einer Regression auf Ihre historischen Werte:

Weiterhin ist es oftmals sinnvoll, nicht eine Zeitreihe y zu prognostizieren, sondern stattdessen die Zeitreihe y‘ der Differenzen:

Letztere hat oft bessere Eigenschaften und aus einer Prognose von y‘ lässt sich leicht eine von y erstellen. Die Differenzenbildung kann mehrfach erfolgen.

 

Eine besonders flexible Modellklasse bilden die sogenannten ARIMA-Modelle (autoregressive integrated moving average model). Sie modellieren den künftigen Wert von y‘ als Summe einer Regression auf vergangene Werte von y‘ und einem gewichteten Mittelwert der historischen Fehler e:

Für die Kalibrierung eines solchen Modells müssen zunächst geeignete Werte für p und q und für die Anzahl der Differenzenbildungen d bestimmt werden. Danach können optimale Werte für die αs, βs und c durch die Methode der kleinsten Quadrate oder durch Maximum-Likelyhood bestimmt werden. Für die Bestimmung von p ist der oben gezeigte Autokorrelationsgraph hilfreich. Weiterhin wird in vielen Softwarepaketen eine automatische Kalibrierung von ARIMA-Modellen zur Verfügung gestellt.

 

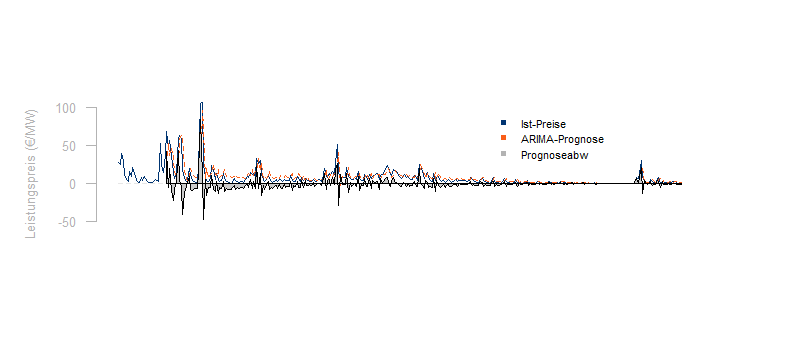
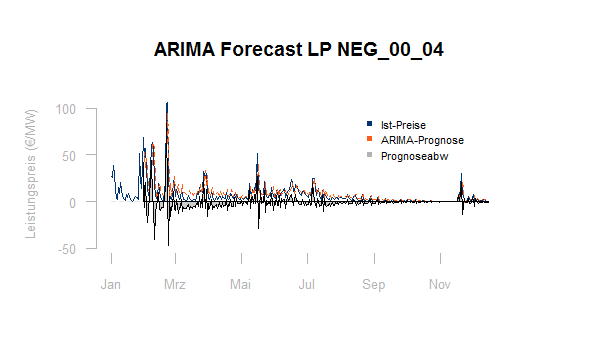
Hier für die bereits oben gezeigten Regelenergiepreise eine Prognose des Folgewertes auf Basis der jeweils verfügbaren historischen Daten mit einem ARIMA-Modell:

 

Wie man sieht, stellt die Prognose von Regelpreisen durchaus eine Herausforderung dar. Die Prognoseabweichung bleibt im Maximum unter der Abweichung der einfachen Fortschreibung des letztgemessenen Wertes:

Ist die raffiniertere Prognose aber wirklich besser?

Messung der Prognosegüte

Sollen nur zwei Prognosemodelle für dieselbe Variable verglichen werden, so kann man die bereits zur Kalibrierung der Modelle verwendete quadratische Abweichung betrachten.

1. Kennzahlen zur Messung der Prognosegüte

Vergleicht man zwei Prognoseverfahren für y, so ist das Verfahren besser, für das die quadratische Abweichung von Prognose und Ist kleiner ist:

Für die gerade verglichenen Methoden zur Vorhersage der Regelpreise (ARIMA und einfache Fortschreibung) ergibt sich tatsächlich, dass das ARIMA-Modell geringfügig besser ist.

 

Als Kennzahl wird oft der mittlere quadratische Fehler (MSE, mean squared error) betrachtet:

Die Wurzel hieraus ergibt RMSE, den Root Mean Squared Error.

 

Es kann auch einfach der Mittelwert der absoluten Abweichungen (MAE, Mean Absolute Error) betrachtet werden:

Für diese Kennzahl schlägt die einfache Fortschreibung das ARIMA-Modell.

 

Diese einfachen Kennzahlen hängen von der Einheiten und absoluten Größenordnung der zu prognostizierenden Variable ab und eignen sich somit nicht zur generellen Beurteilung von Prognosequalität. Als ein normiertes Fehlermaß schlagen Hyndman and Koehler vor, den Fehler eines Prognosemodells im Verhältnis zu dem Fehler einer einfachen Fortschreibung zu messen.

 

Die Prognosequalität von linearen Regressionsmodellen wird üblicherweise mit dem Bestimmtheitsmaß R² oder dem adjustierten Bestimmtheitsmaß R̄² gemessen.

2. Kalibrierungs- und Testdaten

Die Prognosequalität kann nur an Daten getestet werden, die nicht für die Kalibrierung des Modells verwendet wurden. Somit müssen bei Entwicklung eines Prognosemodells zunächst die verfügbaren Daten in Daten zur Kalibrierung und Testdaten aufgeteilt werden.

 

Für die Fortschreibung von Zeitreihen, insbesondere wenn die Daten eine Saisonalität beinhalten, bleibt meist nichts übrig als diese Aufteilung entlang der Zeitachse vorzunehmen. In die Prognose nachfolgender Zeiträume dürfen nur davorliegende Daten eingehen. Somit wird das Modell jeweils mit den Daten bis zum Zeitpunkt t_i kalibriert und hiermit der Wert zum Zeitpunkt t_i+1 vorhergesagt. Man erhält einen Prognosefehler für jedes i abgesehen von einem Zeitfenster am Anfang, dass als minimal angesehen wird, um eine Kalibrierung sinnvoll vornehmen zu können.

 

Soll ein Regressionsmodell oder eine Kalibrierung beispielsweise der Sigmoidfunktion getestet werden, so ist die zeitliche Abfolge der historischen Daten nicht relevant. Das Testset kann dann zufällig gewählt werden. Insbesondere ist das folgende Vorgehen möglich:

• Wähle die Beobachtung i als Testmenge
• Kalibriere das Modell aus allen Daten ohne die Beobachtung i
• Werte den Prognosefehler i für die Beobachtung i aus
• Ermittle den mittleren Fehler über alle möglichen i

3. Weitere Maßnahmen zur Beurteilung der Prognosequalität

Mathematische Kennzahlen zur Beurteilung der Prognosequalität haben oft Schwächen. Sie erkennen beispielsweise nicht, wenn der Zusammenhang zwischen der abhängigen, zu prognostizierenden Variable und den unabhängigen Variablen, die zur Prognose verwendet werden, nur in einem gewissen Zeitfenster gilt und danach zusammenbricht. Die bekannte Kennzahl R² ist Null für eine lineare Regression, wenn der Zusammenhang zwischen den Variablen vorhanden aber nicht linear ist.

 

Somit ist es immer sinnvoll, für die Testdaten die Prognose gegen Ist zu plotten, um die Prognosequalität zu beurteilen. Ebenso sollte der Rest, d.h. die Abweichung des Forecasts vom Ist geplottet werden und mit Punkteplot auf noch vorhandene Abhängigkeiten von den unabhängigen Regressionsvariablen geprüft werden.

 

Idealerweise ist die Restzeitreihe White Noise, d.h. sie repräsentiert eine Zufallsvariable:

• ohne Autokorrelation
• mit Erwartungswert Null
• mit konstanter Varianz

Ist der Erwartungswert der Restzeitreihe ungleich Null, so sollte der Erwartungswert der Prognose hinzugefügt werden. Ist die Restzeitreihe autokorreliert, so ist möglicherweise die Betrachtung einer Differenzzeitreihe (s.u) sinnvoll.

 

Verschiedene mathematische Transformationen sind hilfreich, wenn die Ursprungsdaten bzw. die Restzeitreihe autokorreliert sind oder eine nicht konstante Varianz zeigen. Hierzu zählen:

• die Logarithmierung, wenn die Varianz proportional zum Wert ist
• die Box-Cox-Transformationsfamilie, wenn die Varianz mit dem Wert steigt
• die Betrachtung der Differenzzeitreihe y_i – y_i-1

4. Wirtschaftliche Bewertung der Prognoseabweichung

Zu guter Letzt sollte bei der Beurteilung des Prognosefehlers auch immer die wirtschaftliche Relevanz in Betracht gezogen werden. Sie ist letztendlich die Messlatte dafür, ob sich eine Investion in die Verbesserung der Prognosequalität lohnt. Für die Tagesprognose ergeben sich die Kosten K aus dem Prognosefehler aus dem folgenden Skalarprodukt (Summenprodukt):

dabei ist:

P die Prognosezeitreihe
I die Istzeitreihe
EEX die Spotpreiszeitreihe der EEX
REBAP die Ausgleichsenergiepreiszeitreihe

Wird zuviel prognostiziert, so wird die Überschussmenge am Spotmarkt gekauft (Aufwand, negatives Vorzeichen) und am Ausgleichsenergiemarkt wieder verkauft (Erlöse, positives Vorzeichen). Wird zuwenig prognostiziert, ist es umgekehrt. Für Einspeisung gilt die entsprechende Gleichung mit negativem Vorzeichen.

 

Geht man davon aus, dass sowohl die Prognoseabweichung P – I im Mittelwert Null ist (dies sollte der Anspruch sein) als auch die Abweichung zwischen Spot- und Ausgleichsenergiepreisen REBAP – EEX (Arbitragefreiheit), so sind die erwarteten Kosten K:

Die Korrelation zwischen Prognoseabweichung und dieser Preisdifferenz ist für manche Marktteilnehmer (insbesondere bei der Prognose von Windeinspeisung) immer positiv, in diesem Fall entstehen aus der Prognoseabweichung systematisch Kosten und nicht nur Ergebnisrisiken.

Auch bei einer Prognose von Regelpreisen zählt letztendlich die Optimierung der Erlöse. Danach müssen die Prognoseparameter auch kalibriert werden.

Ausblick und weiterführende Links

Eine ausführliche Einführung in das Thema Forecasting bietet das Onlinebuch zum Thema Forecasting von Rob J. Hyndman und George Athanasopoulos, von dem dieser Artikel viel Inspiration erhalten hat. Von Hyndman wurde auch eine Vielzahl von Forecastverfahren und zugehörigen automatischen Kalibrierungen in R bereitgestellt. Als weitere für die Energiewirtschaft wichtige Tools und Verfahren findet man in dem Buch:

• eine kurze Einführung in Neuronale Netze mit R
• ein Kapitel zu hierarchischen Prognosen

Ein sehr zentrales Thema ist in der Energiewirtschaft weiterhin die Zerlegung von Zeitreihen in Trend und Saisonalität. Oftmals – wie bei HPFC-Modellen – werden generelle Preisniveaus aus Terminpreisen entnommen, während die Tages- und Wochenstruktur aus historischen Daten extrahiert werden sollen. Auch hier bietet das erwähnte Onlinebuch eine kleine Einführung, die meist nicht ausreichen wird. Weiter führt der Artikel STL: A Seasonal-Trend Decomposition Procedure Based on Loess von Cleveland, Rae und Terpenning. Eine Adaption der dort entwickelten Ideen ist der HPFC-Artikel.

 

Gerade bei der Prognose temperaturabhängiger Lasten wie Gas und Fernwärme besteht typischerweise das Problem, dass die unabhängigen Variablen, mit deren Hilfe die Last prognostiziert werden soll, untereinander hoch korreliert sind (Temperatur, Vortagestemperatur, Vortagesmenge, Globalstrahlung …). Dies führt die klassische multilineare Regression schnell an die Grenzen. Sichtbar relevante zusätzliche Variablen werden als irrelevant aussortiert. Ein möglicher Ansatz sind hier dimensionsreduzierende Verfahren wie die Hauptkomponentenanalyse (PCA). Viele Artikel zur Anwendung solcher Verfahren findet man bei R-Bloggers.